Class on April 26 2019
Two of Chris' graduate students (Loes and Nicole) ran another team speed round of the slasher game, while stopping to take a deeper reflection on steps we ran out of
time to discuss in the previous class:
Loes pointed out that if there is no hydrostatic pressure in the x3 direction, then there is only Po pressure in the x3 direction.
When considering the immateriality of a squared term, the square can be brought into the parentheses: (x/y)2 = (x2/y2)
When Bousinesq drives ▽ · u to 0 in the mass equation, the remaining terms in the mass equation must be 0, so they can be eliminated from the momentum equations.
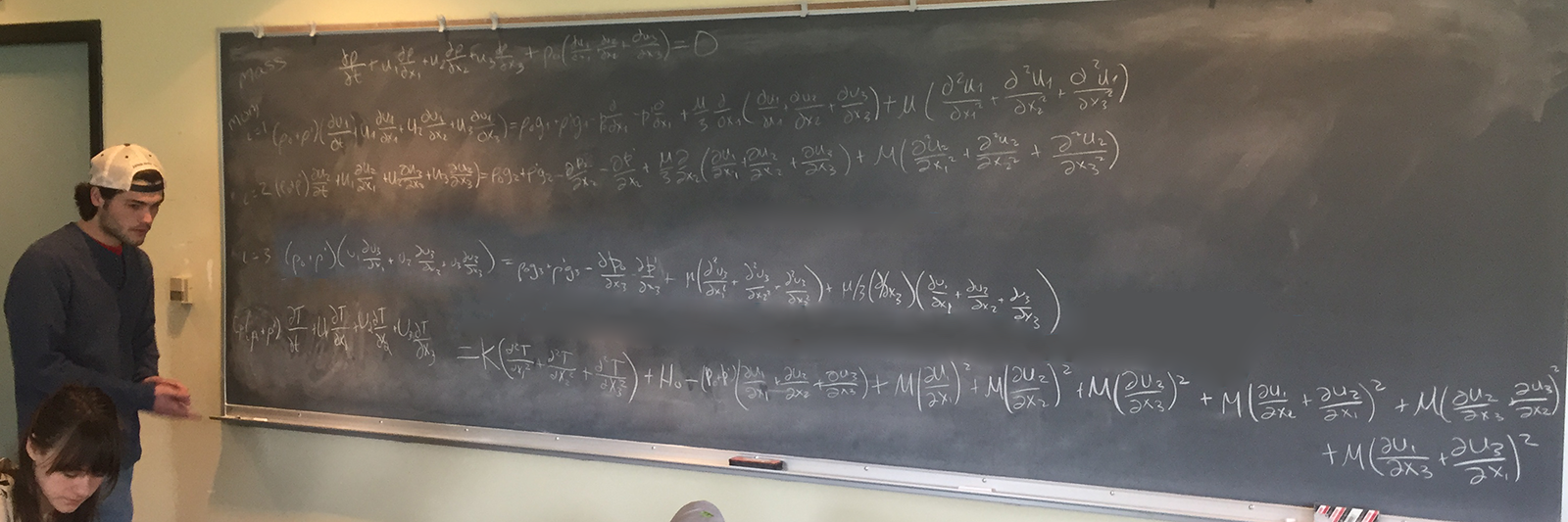
The uniform flow assumption means we are only caring about a bounded region of the overall study area:
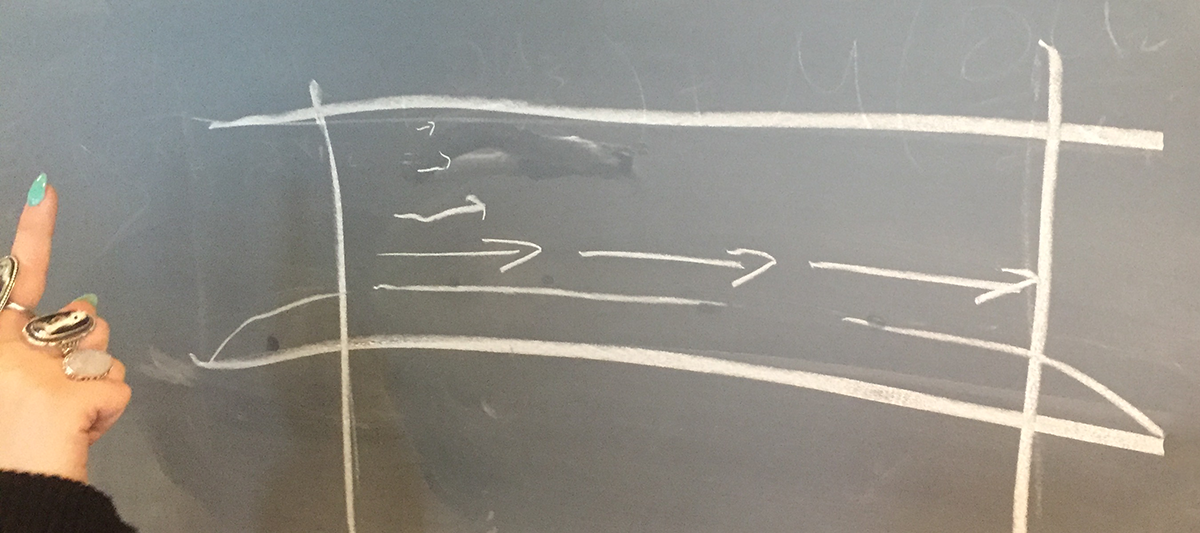
so that the variable flow outside of the bounded region is immaterial to the calculations we are making for the bounded.
Loes reviewed the process by which the remaining simultaneous equations after the slasher game (left of the blackboard below) were solved so that students could embed the results in MATLAB code.
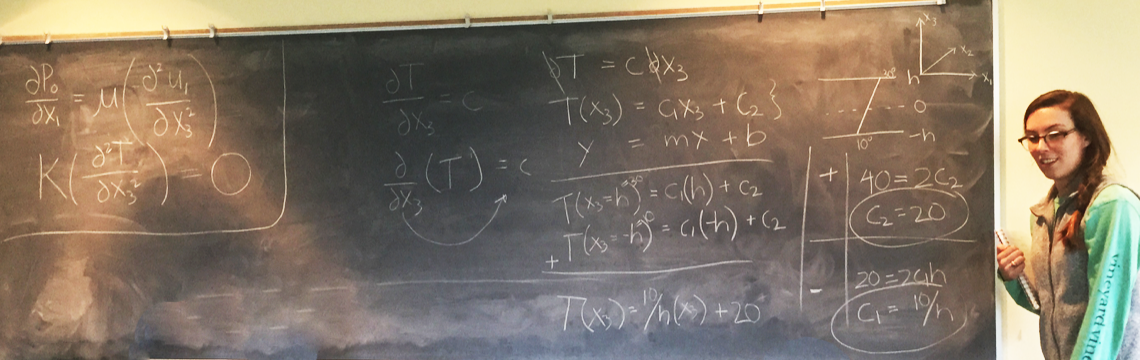
Working on the equation δT/δx3 = C (where C is a constant):
1. multiply both sides of the equation by δx3
2. divide both sides of the equation by δ
3. use two constants C1 and C2 to get the equation in the form of a line (y = mx + b)
4. create two equations using h (distance up from mid-depth line) and -h (distance down from mid-depth line)
5. plug in T(h)=30 for ocean surface and T(-h)=10 for bottom
6. solve the two equations to find the constants (C1 = 10/h, C2 = 20)
Now test the equation T(x3) = 10/h * x3 + 20 for reasonableness:

The derived equation gives the vertical flow profile we expect from our overall understanding of Narragansett Bay mechanics:
Loes pointed out that if there is no hydrostatic pressure in the x3 direction, then there is only Po pressure in the x3 direction.
When considering the immateriality of a squared term, the square can be brought into the parentheses: (x/y)2 = (x2/y2)
When Bousinesq drives ▽ · u to 0 in the mass equation, the remaining terms in the mass equation must be 0, so they can be eliminated from the momentum equations.
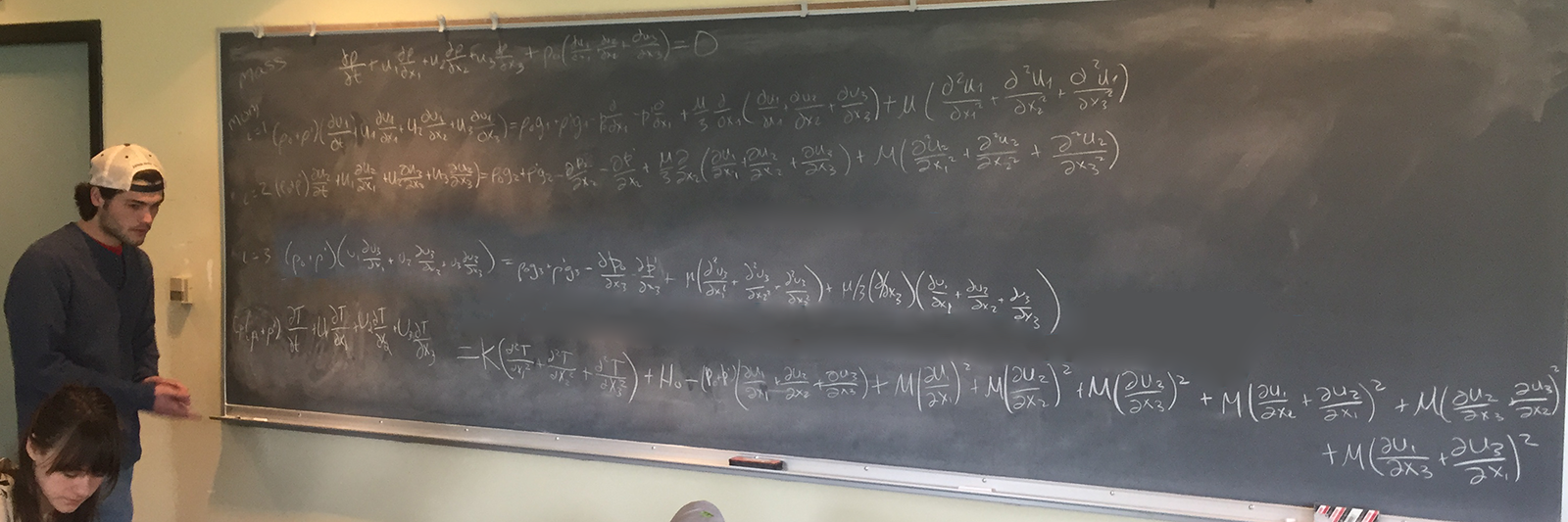
The uniform flow assumption means we are only caring about a bounded region of the overall study area:
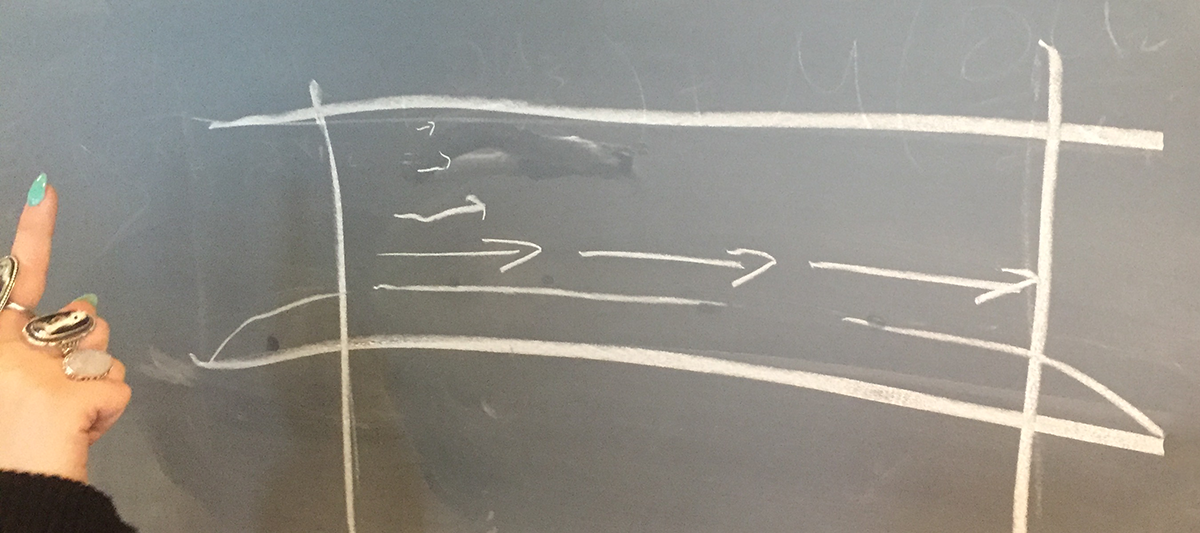
so that the variable flow outside of the bounded region is immaterial to the calculations we are making for the bounded.
Loes reviewed the process by which the remaining simultaneous equations after the slasher game (left of the blackboard below) were solved so that students could embed the results in MATLAB code.
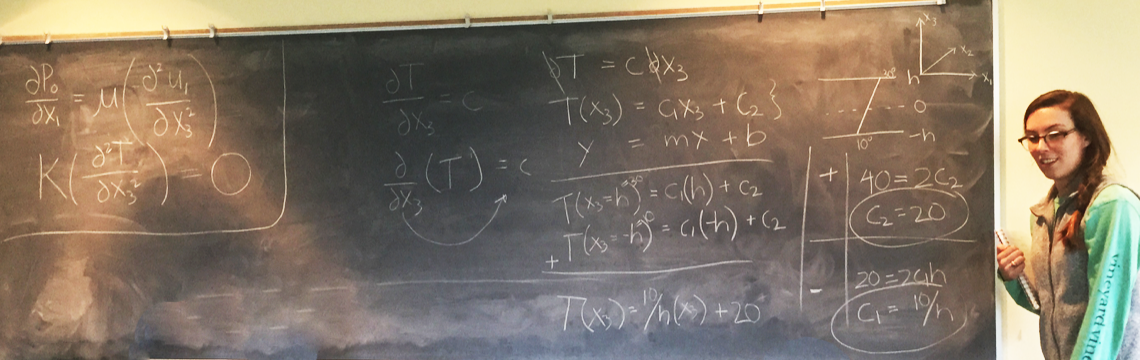
Working on the equation δT/δx3 = C (where C is a constant):
1. multiply both sides of the equation by δx3
2. divide both sides of the equation by δ
3. use two constants C1 and C2 to get the equation in the form of a line (y = mx + b)
4. create two equations using h (distance up from mid-depth line) and -h (distance down from mid-depth line)
5. plug in T(h)=30 for ocean surface and T(-h)=10 for bottom
6. solve the two equations to find the constants (C1 = 10/h, C2 = 20)
Now test the equation T(x3) = 10/h * x3 + 20 for reasonableness:
x3 T(x3)
h | 30
h/2 | 25
0 | 20
-h/2 | 15
-h | 10
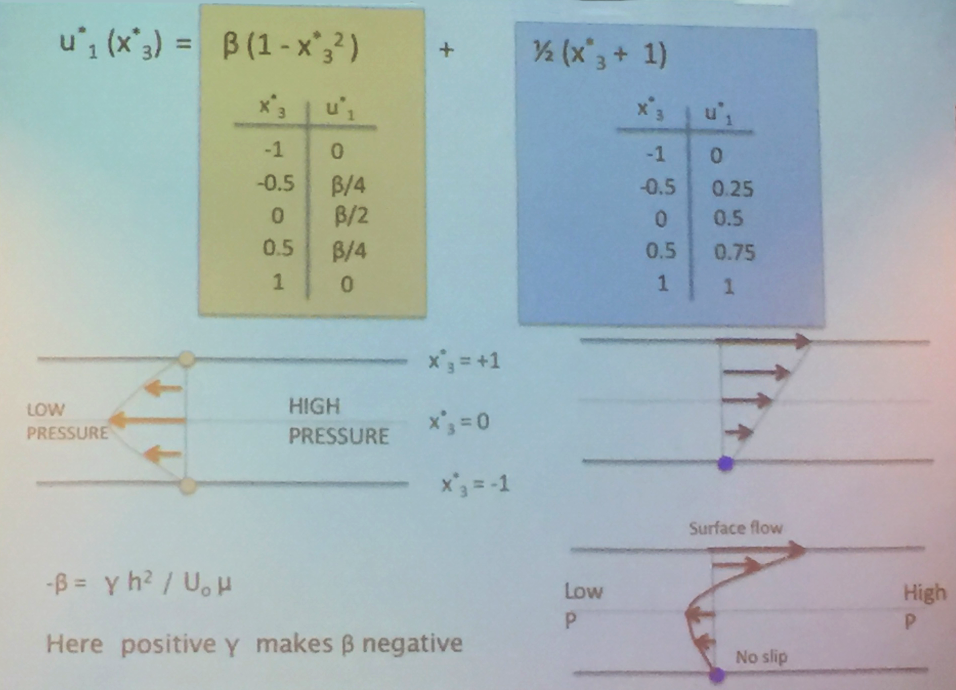
But Chris then suggested students use a lateral pressure gradient in x1 for Homework #7 and use the character γ
(gamma) to denote it. An equation for lateral flow as a function of depth could then be derived through mathematical transformations,
u*1(x*3):

The derived equation gives the vertical flow profile we expect from our overall understanding of Narragansett Bay mechanics:


