Class on April 22 2019
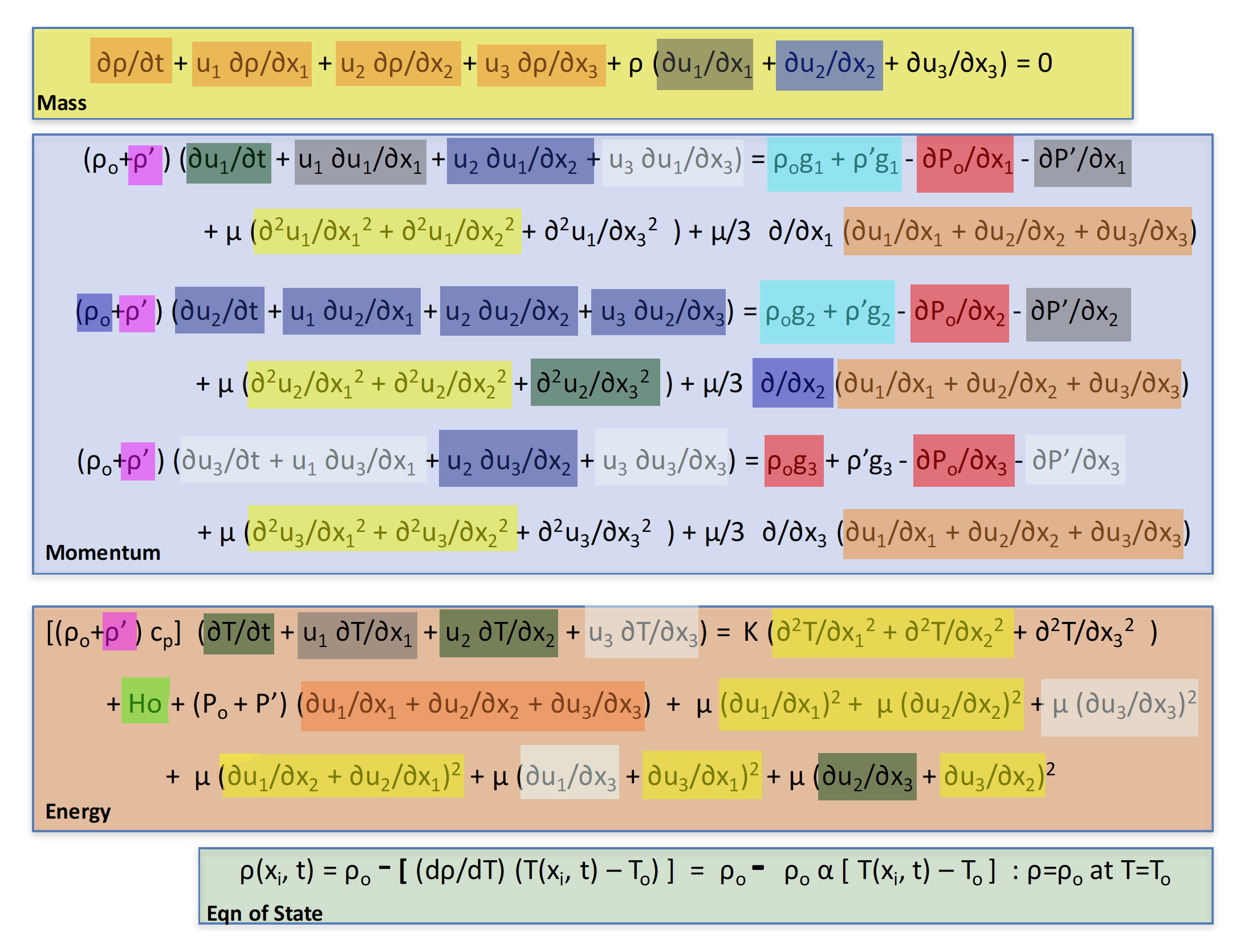
Chris played the slasher game with the students. First he broke the class into three teams. Then he reviewed the situation to be modeled by formula: flow in the West Passage of
Narragansett Bay (using X1 as the north-south length of the passage and X3 as depth). Chris had the students write the full set of equations
(team 1 wrote momentum x1 and diffusion, team two wrote momentum x2 and advection, and team three wrote momentum x3 and conservation of mass)
for calculating temperature flow (as built up in the first 22 class periods):
where ρ represents the surface stress on each parcel of water, P represents thermal pressure, g3 represents gravity, λ represents bulk viscosity, Κ represents thermal diffusivity, μ represents dynamic viscosity, and cp represents heat capacity.
The bottom equation represents the starting state for temperature in the model area (the cumulation of all past activity up to the start of the model, T0).
Teams then took turns identifying reasonable simplifying assumptions that removed terms from the equations as having no relevance or immaterial impact (Chris assigned points based on insight value — colors below show the slashing terms in the order below):
GREEN: No heat sources/sinks
LIGHT BLUE: x3 is vertical axis (x1, x2 are the horizontal plane)
RED: Po is hydrostatic pressure from weight of overlying fluid
YELLOW: H << L & W
MAGENTA: Bousinesq - p0>>>>p'
ORANGE: Bousinesq assuming density is constant in Mass Conservation, but not in momentum
DARK BLUE: Assume no flow in X2
DARK GREEN: Assume water body is in steady state
GREY: The area we are looking at is located FAR from the channel entrance/exit (velocity and thermal boundary layers are fully evolved — UNIFORM FLOW)
WHITE: Assume the upper and lower boundaries (depth of 0 and H) are immermeable so that u3 (flow) is 0.
The terms were removed to leave the final terms to be used in computation (using the colors by reason from above legend):
The resulting terms represent formulas for a reasonable compuation of temperature flux in our class scenario: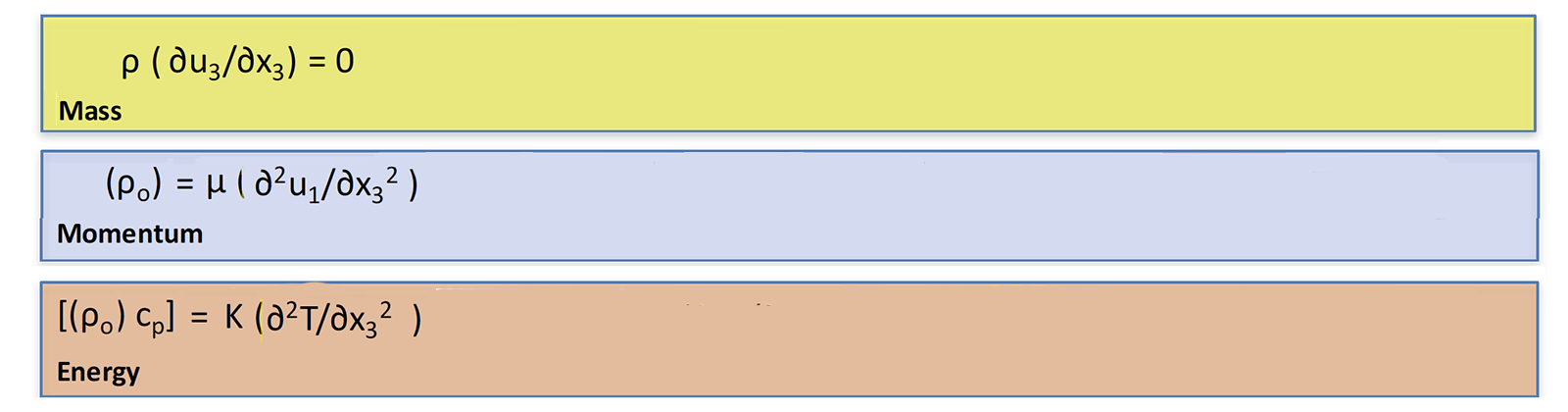
Students are expected to understand all the significant activities that took place in the slasher game in order to be proficient at the oral final.
where ρ represents the surface stress on each parcel of water, P represents thermal pressure, g3 represents gravity, λ represents bulk viscosity, Κ represents thermal diffusivity, μ represents dynamic viscosity, and cp represents heat capacity.
The bottom equation represents the starting state for temperature in the model area (the cumulation of all past activity up to the start of the model, T0).
Teams then took turns identifying reasonable simplifying assumptions that removed terms from the equations as having no relevance or immaterial impact (Chris assigned points based on insight value — colors below show the slashing terms in the order below):
GREEN: No heat sources/sinks
LIGHT BLUE: x3 is vertical axis (x1, x2 are the horizontal plane)
RED: Po is hydrostatic pressure from weight of overlying fluid
YELLOW: H << L & W
MAGENTA: Bousinesq - p0>>>>p'
ORANGE: Bousinesq assuming density is constant in Mass Conservation, but not in momentum
DARK BLUE: Assume no flow in X2
DARK GREEN: Assume water body is in steady state
GREY: The area we are looking at is located FAR from the channel entrance/exit (velocity and thermal boundary layers are fully evolved — UNIFORM FLOW)
WHITE: Assume the upper and lower boundaries (depth of 0 and H) are immermeable so that u3 (flow) is 0.
The terms were removed to leave the final terms to be used in computation (using the colors by reason from above legend):
The resulting terms represent formulas for a reasonable compuation of temperature flux in our class scenario:
Students are expected to understand all the significant activities that took place in the slasher game in order to be proficient at the oral final.
