Class on March 29 2019
Chris reviewed the progression of classes of late. We had spent quite a bit of time deriving the conservation of energy equation
(looking at advection-diffusion along the lines of the Navier-Stokes equations). But we recently turned our attention to the Conservation
of Momentum (and would be moving on to Conservation of Mass upon giving momentum due focus).
Chris took us through the progression we had pursued the previous class, starting with:
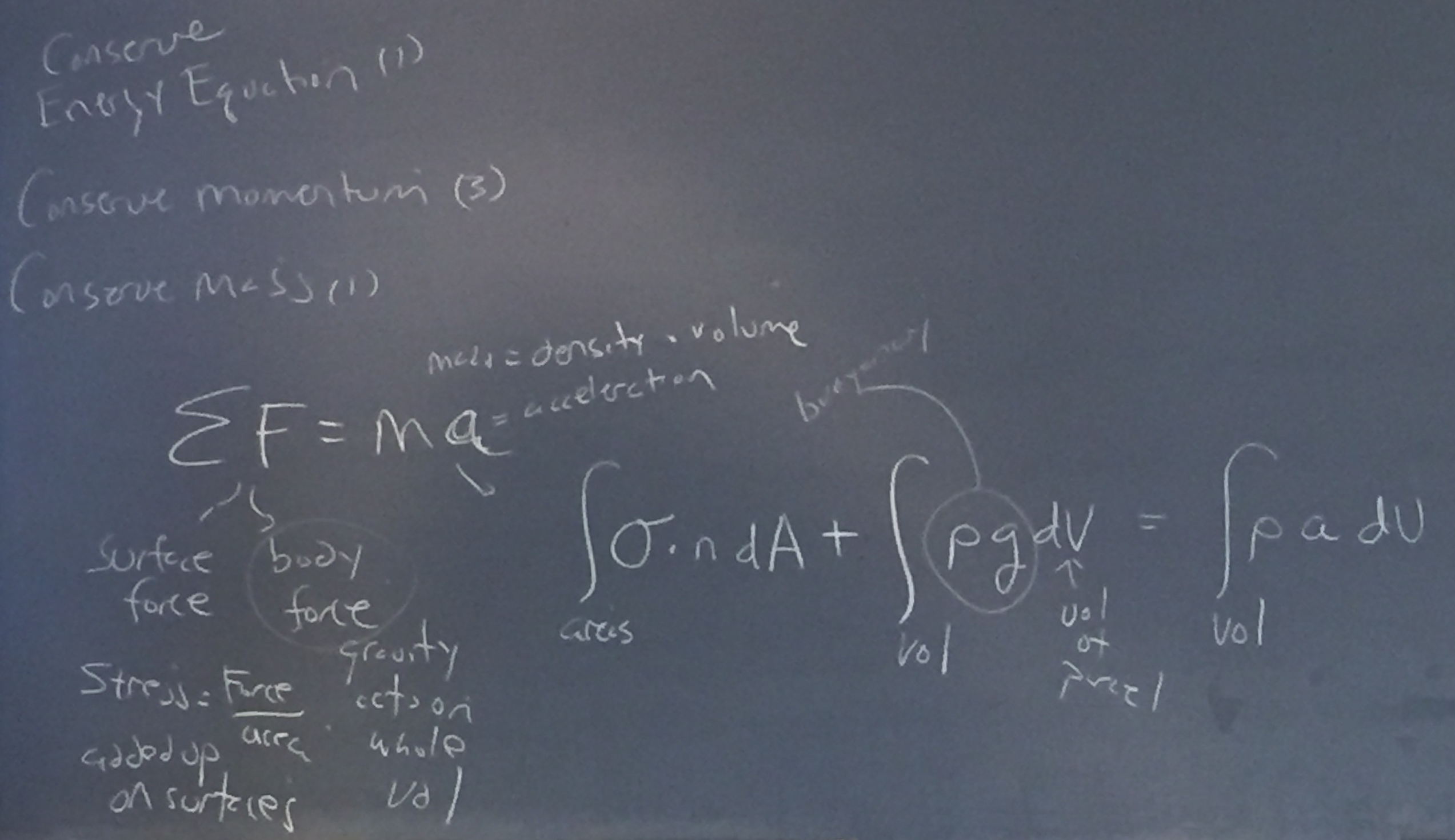
We simplified the first term using Gauss' theorem to approximate the integral of the surfaces with an integral of volume component:
▽ . σ δv
Performing the integral to both sides we get the very useful equation:
▽ . σ + ρ * g = ρ * a
where ▽ . σ is surface force,
ρ * g is body force, and a is acceleration.
Next we worked on the idea of substituting δμ/δa for a and performed some kinesthetic exercises to understand that concept.
Chris reminded us from last class that ρ is the total stress which is the sum of p (pressure) and τ (deviatoric stress)
We categorized stress as causing three kinds of changes:
1. change of location (translation)
2. deformation (change of length if normal, or change of the angle of the sides) 3. change of orientation (rotation)
Chris took a time out to point out the difference between a solid and liquid in terms of mechanics. When a stress is applied to a solid, the result reaches an equilibrium where L (the length) can be measured as μ. When stress is applied to a liquid, μ is more appropriately measured as L/t since the stress continues to create change over time as it continues to exist.
Students used play dough to review the nine combinations of stress. For example ρ13 could be represented by:

since the finger represented the x1 component and the hand represented the x3 response.
Students then used a straw to represent the change of a face of the cube. For example:

where the cube rotated by 45 degrees in the x1x2 plane. Chris reviewed the formulation of a cube's translation and rotation in terms of δμ/δx1:
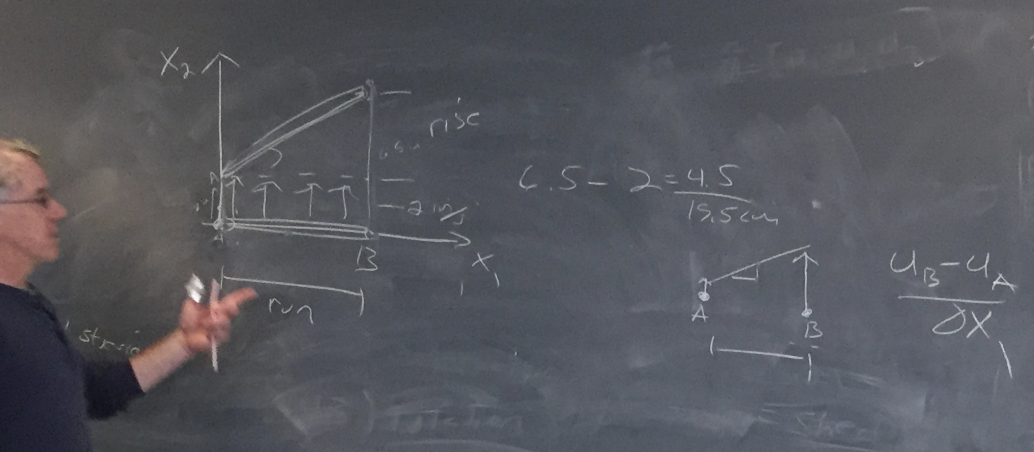
and introduced us to the concept of small incremental strain (whereby the concept of δx1 becomes marginal to the point of being immaterial (hence the 19.5cm even though the rotation looks like it is reducing B - A on the blackboard).
Students then looked at four pencils hinged in a square arrangement by duct tape in order to look at the effect of deformations:

Chris asked students to calculate the relevant δμi/δxj for different axes. For example:
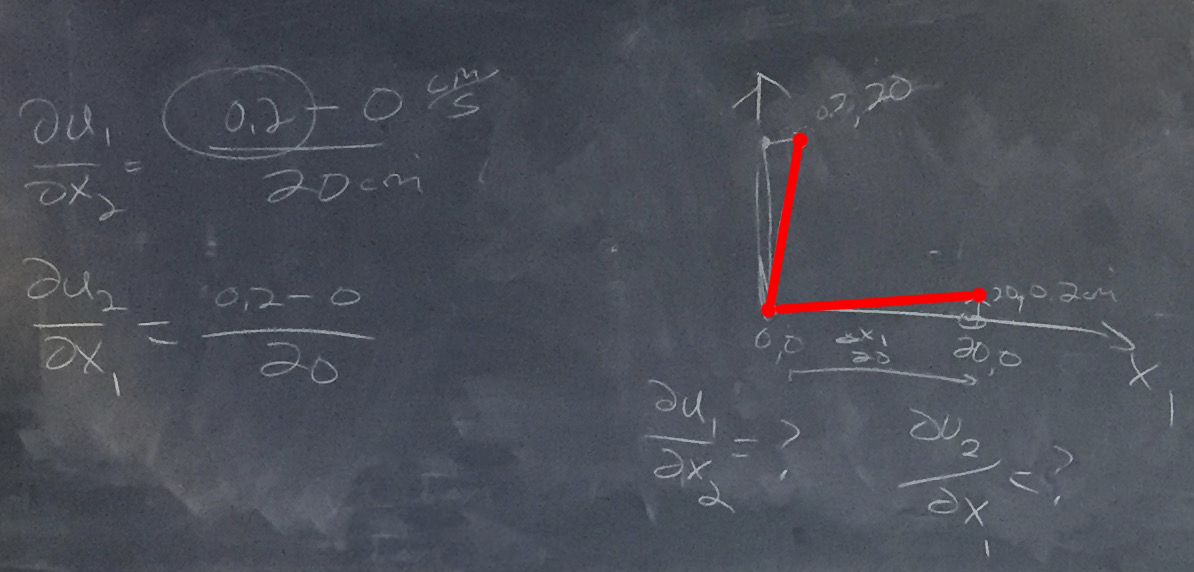
whereby the pencils formed a parallelogram in the x1x2 plane.
Chris brought us back to the nine term matrix we began investigating last class and got the students thinking about how the nine terms in the matrix represented all the possible stresses that could happen to a parcel of water (the normal stresses on the diagonal).

Chris showed an algebraic manipulation to δμi/δxj These stresses are the stresses that maintain the volume of water. The math would continue to add complexity in future classes...
Chris took us through the progression we had pursued the previous class, starting with:
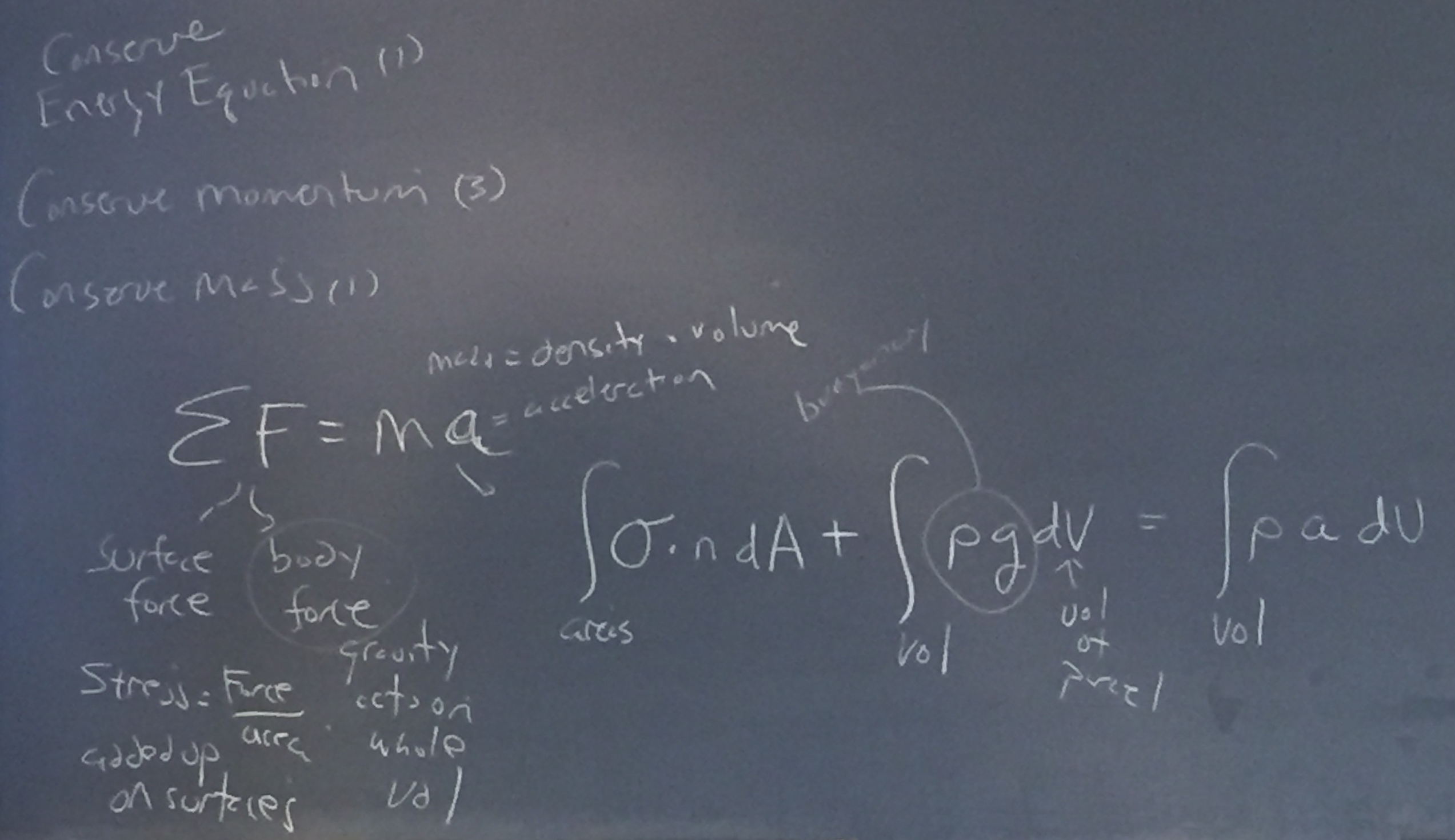
We simplified the first term using Gauss' theorem to approximate the integral of the surfaces with an integral of volume component:
▽ . σ δv
Performing the integral to both sides we get the very useful equation:
▽ . σ + ρ * g = ρ * a
where ▽ . σ is surface force,
ρ * g is body force, and a is acceleration.
Next we worked on the idea of substituting δμ/δa for a and performed some kinesthetic exercises to understand that concept.
Chris reminded us from last class that ρ is the total stress which is the sum of p (pressure) and τ (deviatoric stress)
We categorized stress as causing three kinds of changes:
1. change of location (translation)
2. deformation (change of length if normal, or change of the angle of the sides) 3. change of orientation (rotation)
Chris took a time out to point out the difference between a solid and liquid in terms of mechanics. When a stress is applied to a solid, the result reaches an equilibrium where L (the length) can be measured as μ. When stress is applied to a liquid, μ is more appropriately measured as L/t since the stress continues to create change over time as it continues to exist.
Students used play dough to review the nine combinations of stress. For example ρ13 could be represented by:

since the finger represented the x1 component and the hand represented the x3 response.
Students then used a straw to represent the change of a face of the cube. For example:

where the cube rotated by 45 degrees in the x1x2 plane. Chris reviewed the formulation of a cube's translation and rotation in terms of δμ/δx1:
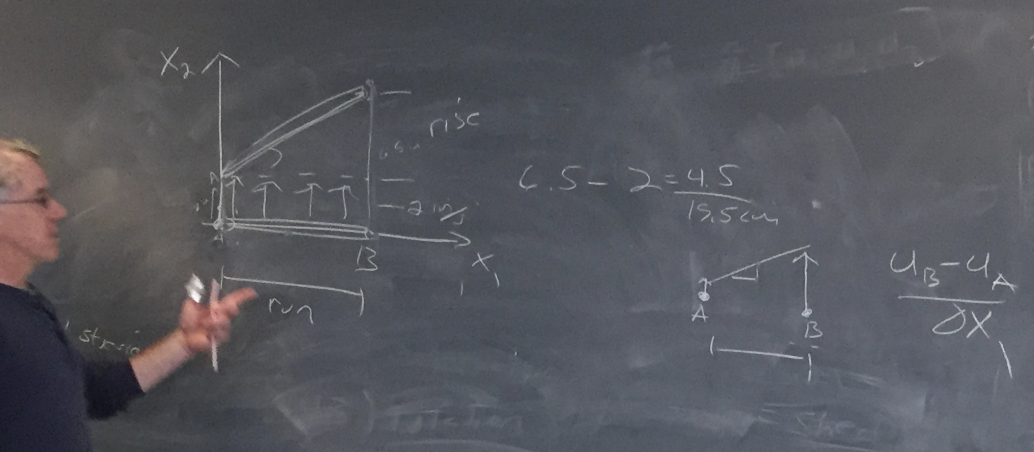
and introduced us to the concept of small incremental strain (whereby the concept of δx1 becomes marginal to the point of being immaterial (hence the 19.5cm even though the rotation looks like it is reducing B - A on the blackboard).
Students then looked at four pencils hinged in a square arrangement by duct tape in order to look at the effect of deformations:

Chris asked students to calculate the relevant δμi/δxj for different axes. For example:
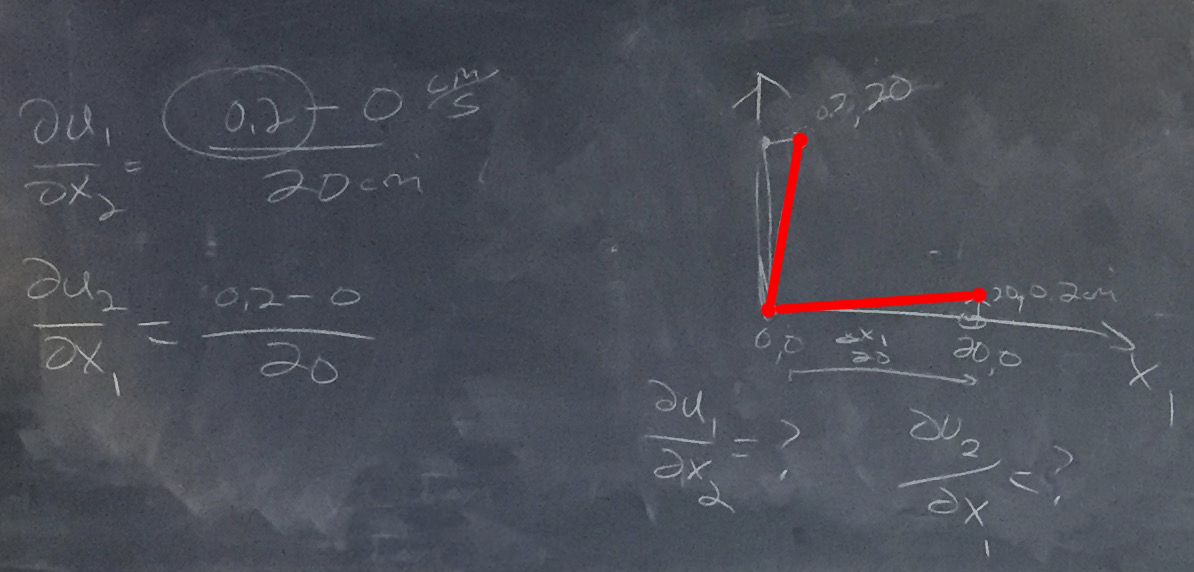
whereby the pencils formed a parallelogram in the x1x2 plane.
Chris brought us back to the nine term matrix we began investigating last class and got the students thinking about how the nine terms in the matrix represented all the possible stresses that could happen to a parcel of water (the normal stresses on the diagonal).

Chris showed an algebraic manipulation to δμi/δxj These stresses are the stresses that maintain the volume of water. The math would continue to add complexity in future classes...

