Class on March 25 2019
Chris reviewed the mechanics of the advection-diffusion simulation exercise one last time, with students behaving as bins with their height as
temperature.

Then he continued providing context for adding advection to the flow analysis for homework #6 (u in x2 and x3)
Advection is different by depth — the u2 term is a function of x3: f(x3)
equation of motion: force on a parcel = mass of the parcel times the acceleration of the parcel:
F = m*a
Force is the sum of surface force (stress) and body force (gravity on complete volume)
We looked at surface forces comprising of pressure (which is uniform in all directions) + deviatoric (normal if perpendicular, sheer if not)
We can describe stress as a rank 2 tensor with magnitude and two directions (direction of the force + the face effected)
Students played with all possible normal and sheer force representations on a paper cube to generate Ti,j as a matrix whereby Tmn is the deviatoric stress of an axis m on a face n (there are nine combinations whereby T11, T22, and T33 are normal). Values can be positive or negative depending on whether the face is in positive or negative coordinates:
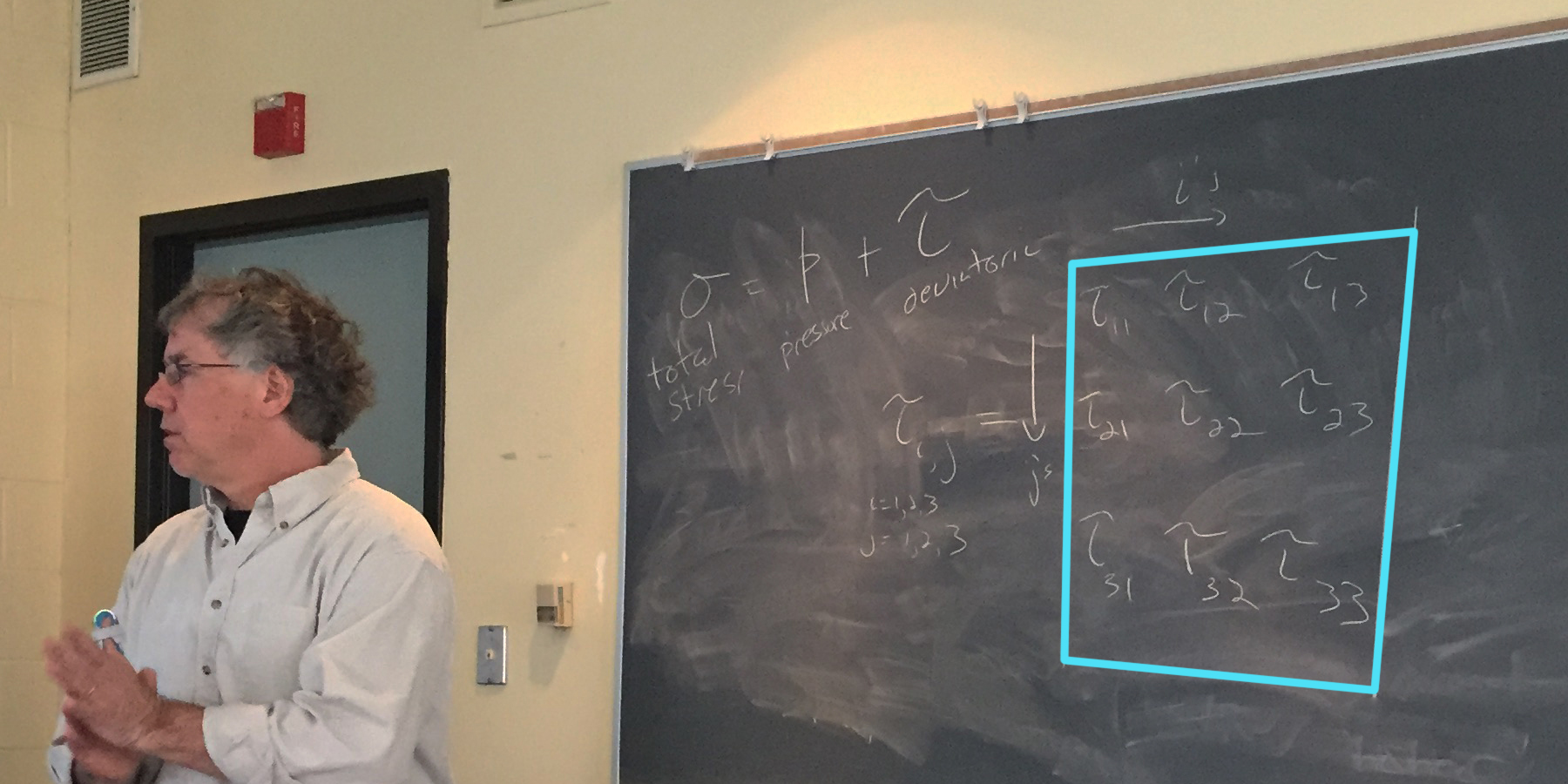
To get the total surface stress, we want to integrate over ▽ . n * δS
which can then simplify by revisiting Gauss' divergence theorem which suggests:
integral of q . n * δS = ▽ . q
as a very good approximation where dS is δx1 δx2
We can then expand F = ma into components body force + surface force (as integrals)
but the integral of δS is hard to mix with δV so we use Gauss' divergence theorem to simplify via:
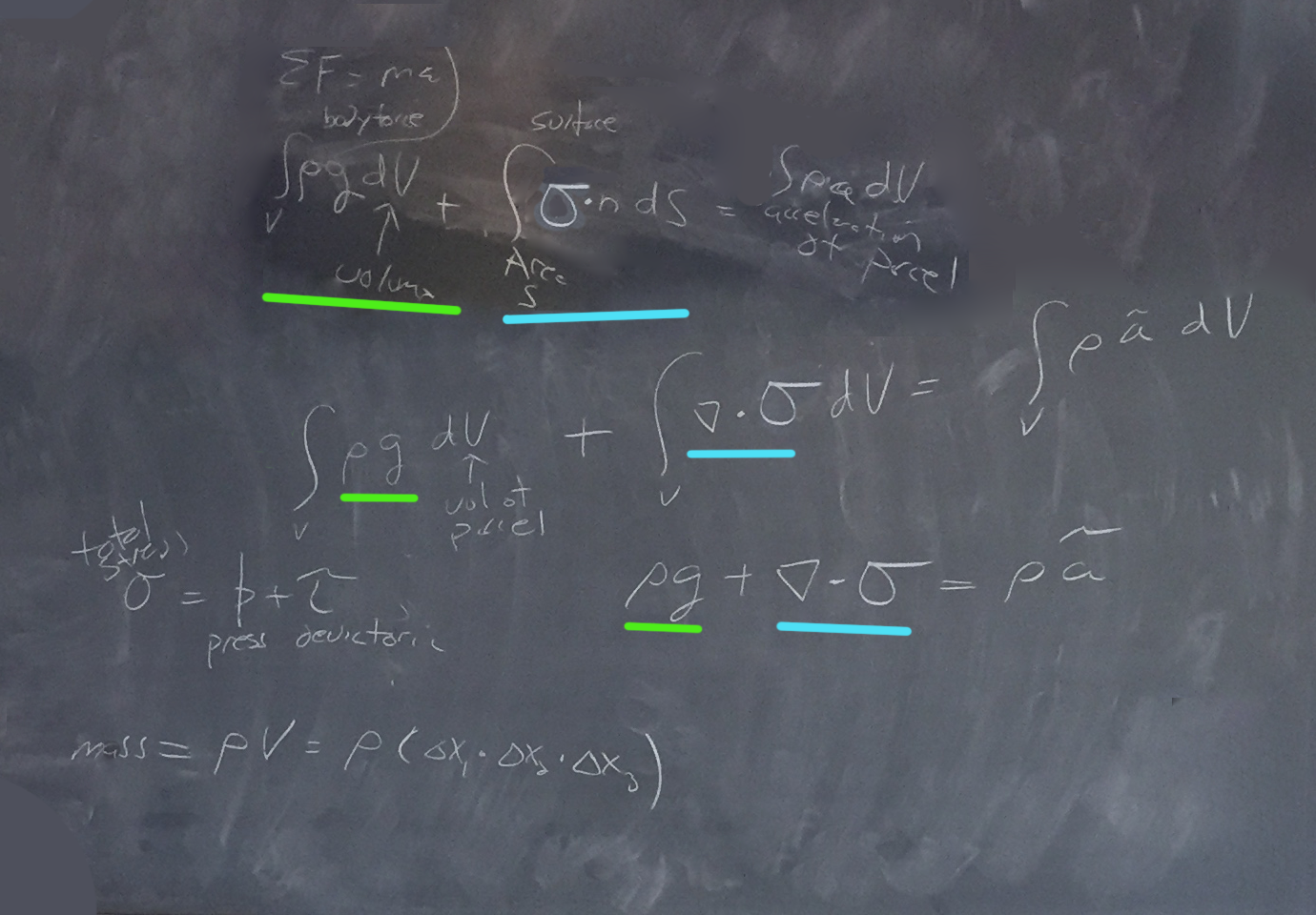
whereby the green is the body force and the blue is the surface force
We end up with an advection formula that we can express in model code, such as the one we are using in homework #6:
u2(x3) = (0.5*B/μ) Z2 + (((Uo/h) - (0.5*B*h/μ))
B is the lateral pressure gradient
h is the height of x3 from the bottom
Z is an array of depths in x3
Uo is the river runoff rate
μ is a viscosity parameter

Then he continued providing context for adding advection to the flow analysis for homework #6 (u in x2 and x3)
Advection is different by depth — the u2 term is a function of x3: f(x3)
equation of motion: force on a parcel = mass of the parcel times the acceleration of the parcel:
F = m*a
Force is the sum of surface force (stress) and body force (gravity on complete volume)
We looked at surface forces comprising of pressure (which is uniform in all directions) + deviatoric (normal if perpendicular, sheer if not)
We can describe stress as a rank 2 tensor with magnitude and two directions (direction of the force + the face effected)
Students played with all possible normal and sheer force representations on a paper cube to generate Ti,j as a matrix whereby Tmn is the deviatoric stress of an axis m on a face n (there are nine combinations whereby T11, T22, and T33 are normal). Values can be positive or negative depending on whether the face is in positive or negative coordinates:
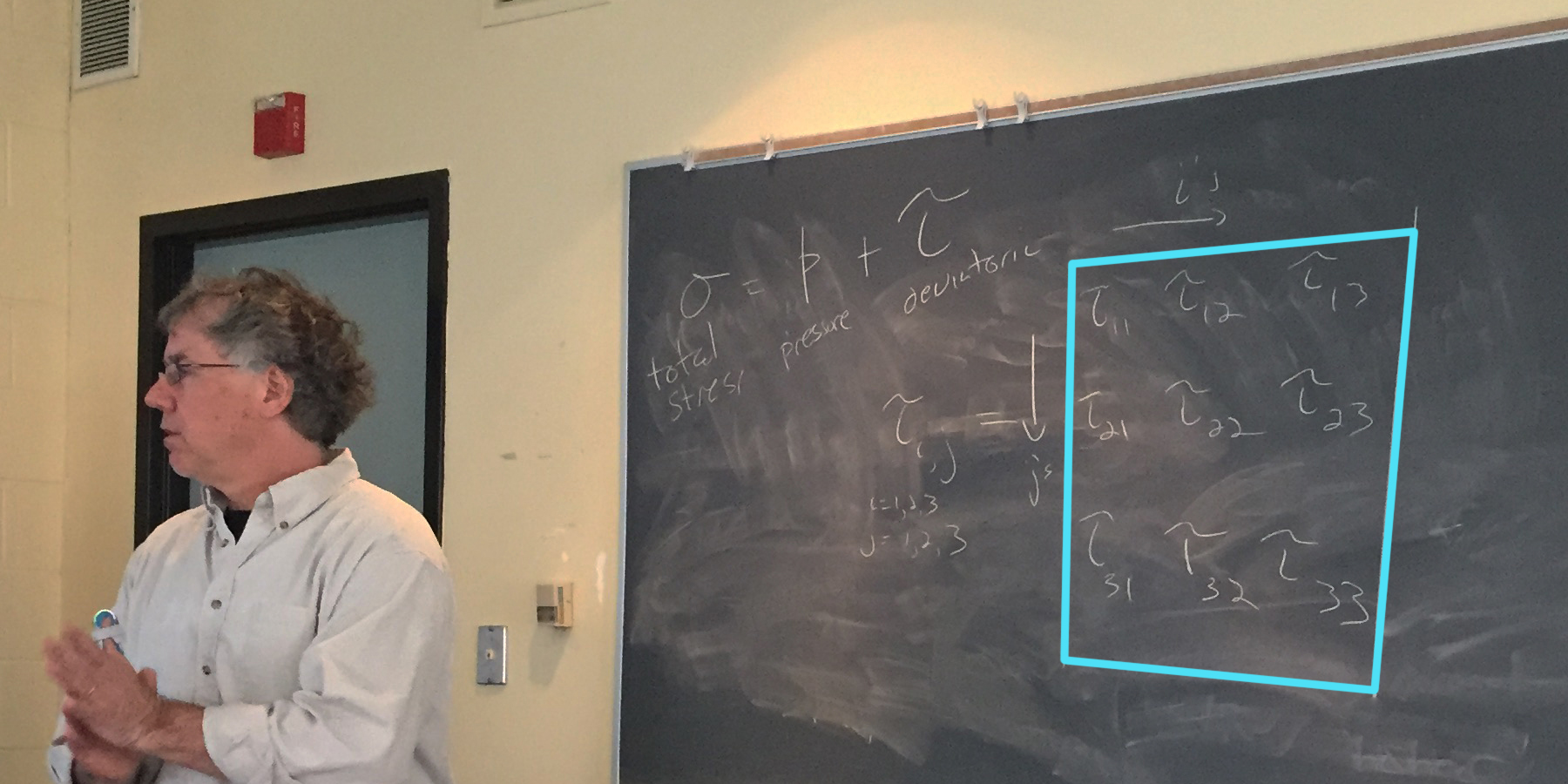
To get the total surface stress, we want to integrate over ▽ . n * δS
which can then simplify by revisiting Gauss' divergence theorem which suggests:
integral of q . n * δS = ▽ . q
as a very good approximation where dS is δx1 δx2
We can then expand F = ma into components body force + surface force (as integrals)
but the integral of δS is hard to mix with δV so we use Gauss' divergence theorem to simplify via:
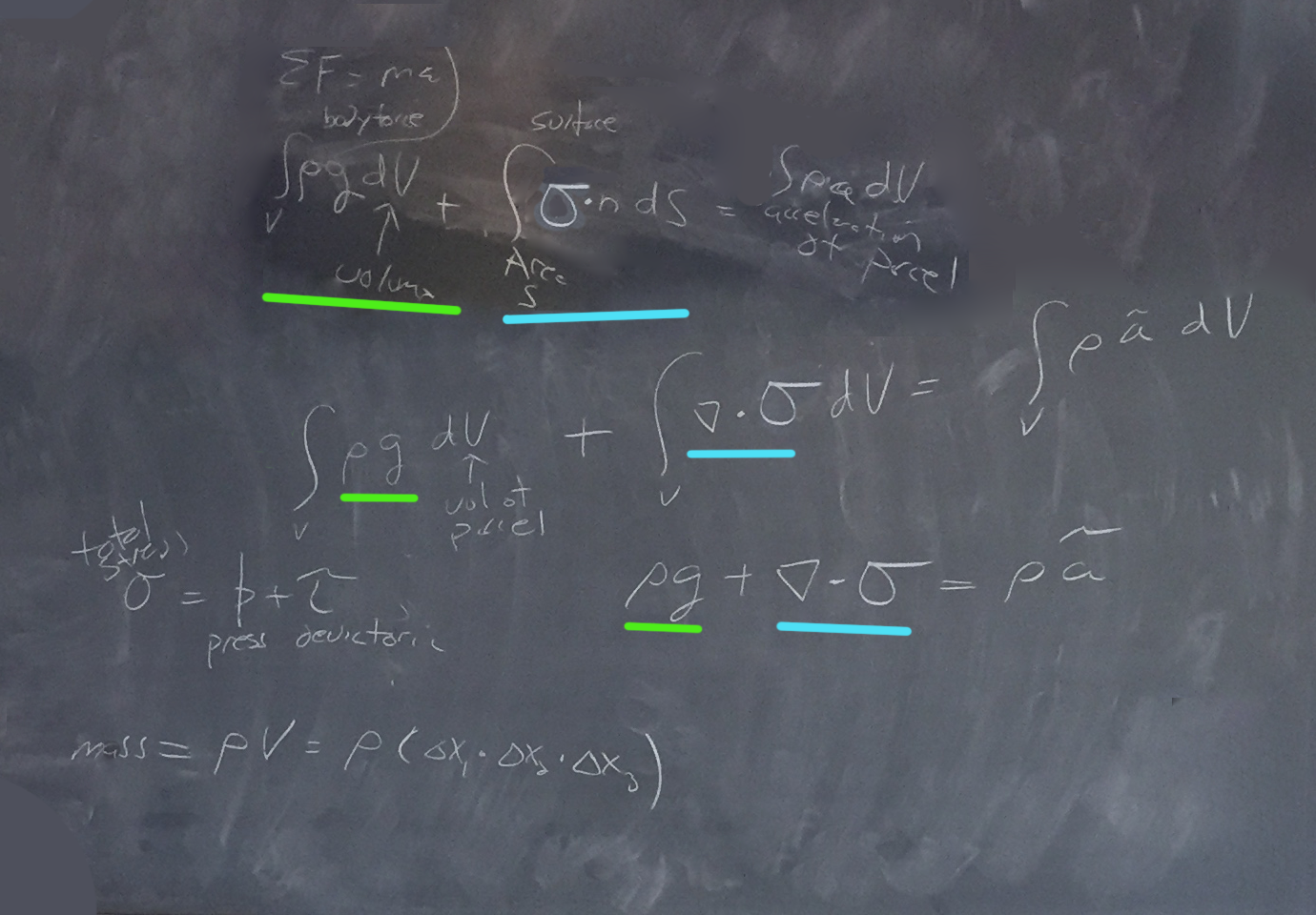
whereby the green is the body force and the blue is the surface force
We end up with an advection formula that we can express in model code, such as the one we are using in homework #6:
u2(x3) = (0.5*B/μ) Z2 + (((Uo/h) - (0.5*B*h/μ))
B is the lateral pressure gradient
h is the height of x3 from the bottom
Z is an array of depths in x3
Uo is the river runoff rate
μ is a viscosity parameter

