Class on February 15 2019
Chris warmed us by reminding us that last class we left of with heat flow v. internal energy v. work
We continued with an investigation of: ρ * cp * dT/dt = ▽ · q + H0 + work
ρ as density
cp as heat capacity
▽ · q is the divergence of heat flow
H0 is the internal heat source
Chris reminded that we have a learning cycle we can engage in at any point:
math -> intuition -> application -> math
Chris also reminded us there were two notations of equal usefulness:
1. vector notation: q~ = K * ▽ T
2. indicial notation: qi = Κ * δT/δxi
K is thermal conductivity
Chris put the students into teams to do ▽ · q, ▽ · q~, and ▽~ · . u~ expansions on the blackboard:
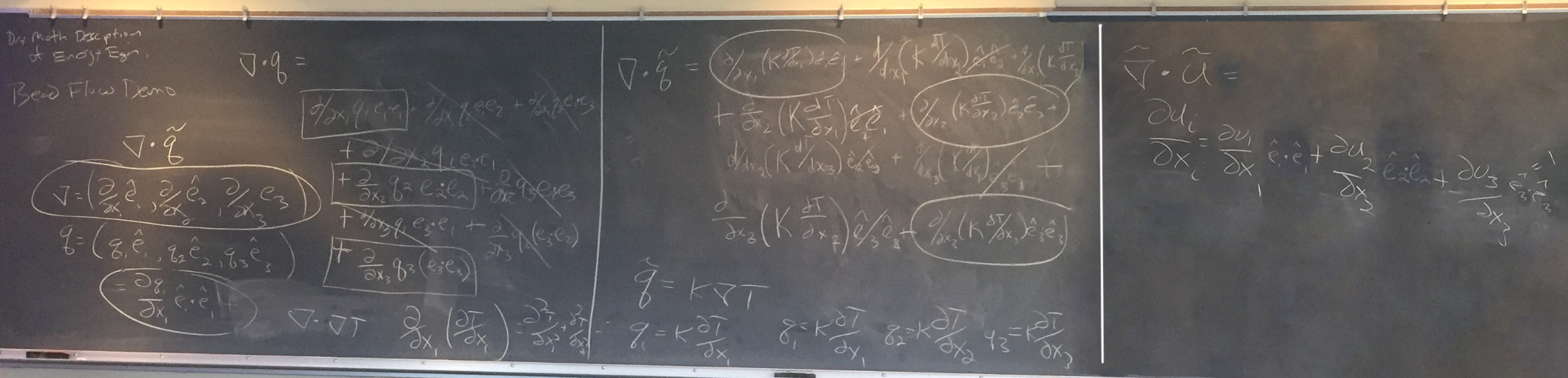
He reminded us to continue to do them long-hand with cancelations until the process feels ingrained enough.
With the energy equations in mind, Chris did another exercise representing lessons from rolling ball demo in physical ocean. Students in teams of four were asked to use plastic piping to represent the flow of heat at the locations in a watershed (Team West's locations shown in purple):
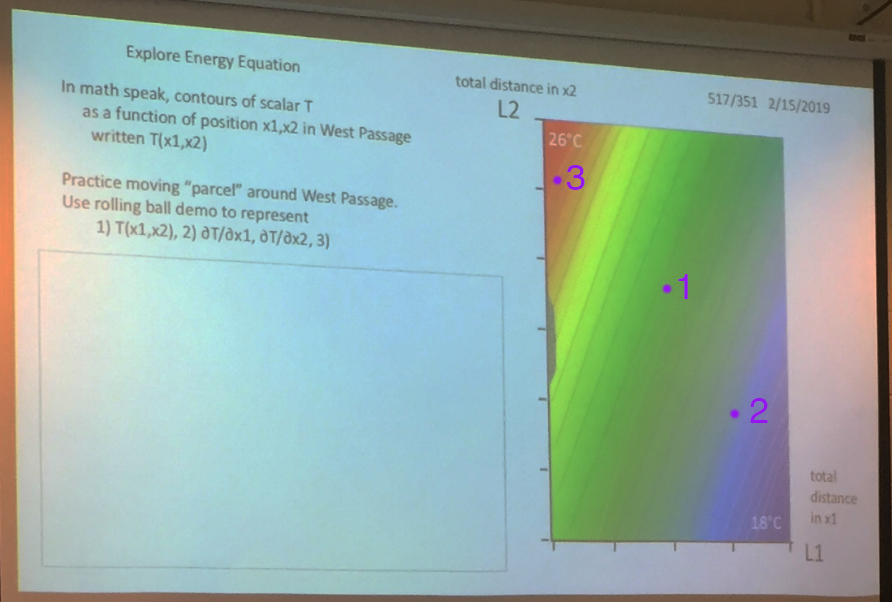
Students found the location based on the dimensions of the classroom and oriented the piping:

Students were asked to answer three questions at each location:
1. How to represent each location in terms of L1 and L2?
2. Is the gradient increasing (+) or decreasing (-) in the directions of L1 (E) and L2 (N)
3. What is the rough magnitude of the heat flow at those locations
Team West provided the answers at the front blackboard:

Students were then asked to quantify the heat flow in terms of a parcel diagrammed as such:
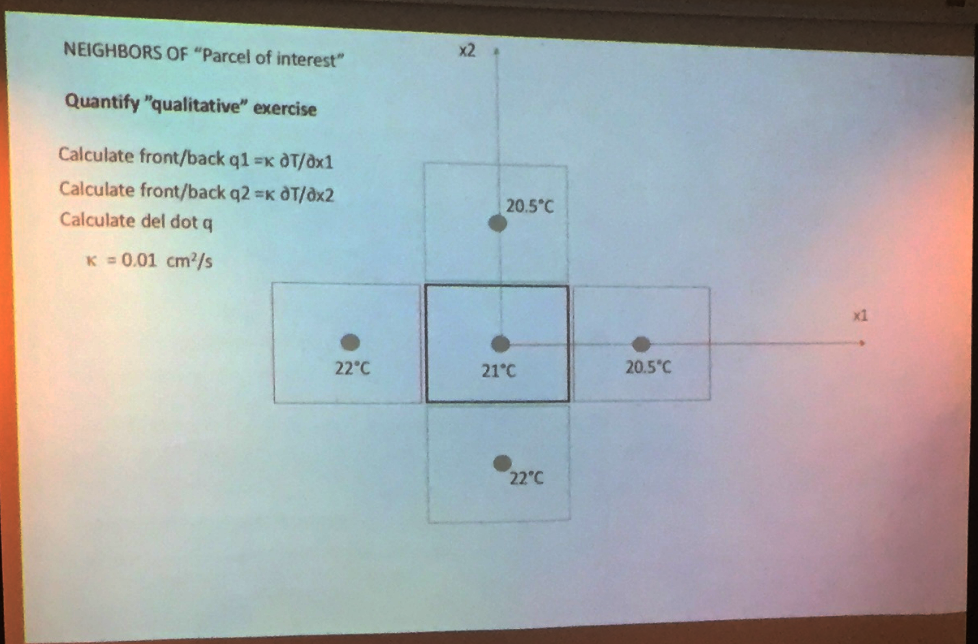
After students worked for ten minutes, Chris provided a relevant equation on the blackboard for students to contemplate:
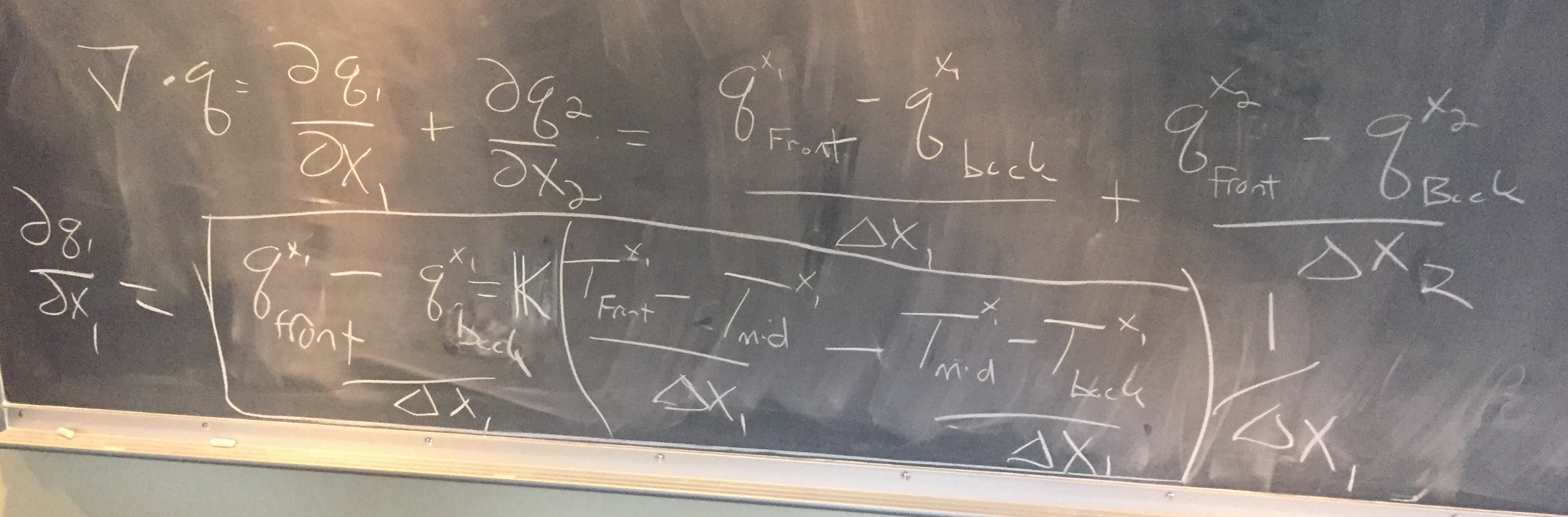
The term front refers to the parcel out front (more east or north) while the term back refers to the parcel behind (more west or south).
The calculations from the above blackboard equations expand as:
1. front/back q1:
front: (.001 cm2/second * -.5 °C /1 cm) = -.005 cm °C/second
back: (.001 cm2/second * -1 °C /1 cm) = -.01 cm °C/second
2. front/back q2:
front: (.001 cm2/second * -.5 °C /1 cm) = -.005 cm °C/second
back: (.001 cm2/second * -1 °C /1 cm) = -.01 cm °C/second
3. ▽ · q:
(-.005 - -.01) + (-.005 - -.01) + 0 = .01 cm °C/second
(just doing flow at the surface so no third term q3)
Chris suggested students ponder on this all weekend until it becomes more familiar and anticipated.
We continued with an investigation of: ρ * cp * dT/dt = ▽ · q + H0 + work
ρ as density
cp as heat capacity
▽ · q is the divergence of heat flow
H0 is the internal heat source
Chris reminded that we have a learning cycle we can engage in at any point:
math -> intuition -> application -> math
Chris also reminded us there were two notations of equal usefulness:
1. vector notation: q~ = K * ▽ T
2. indicial notation: qi = Κ * δT/δxi
K is thermal conductivity
Chris put the students into teams to do ▽ · q, ▽ · q~, and ▽~ · . u~ expansions on the blackboard:
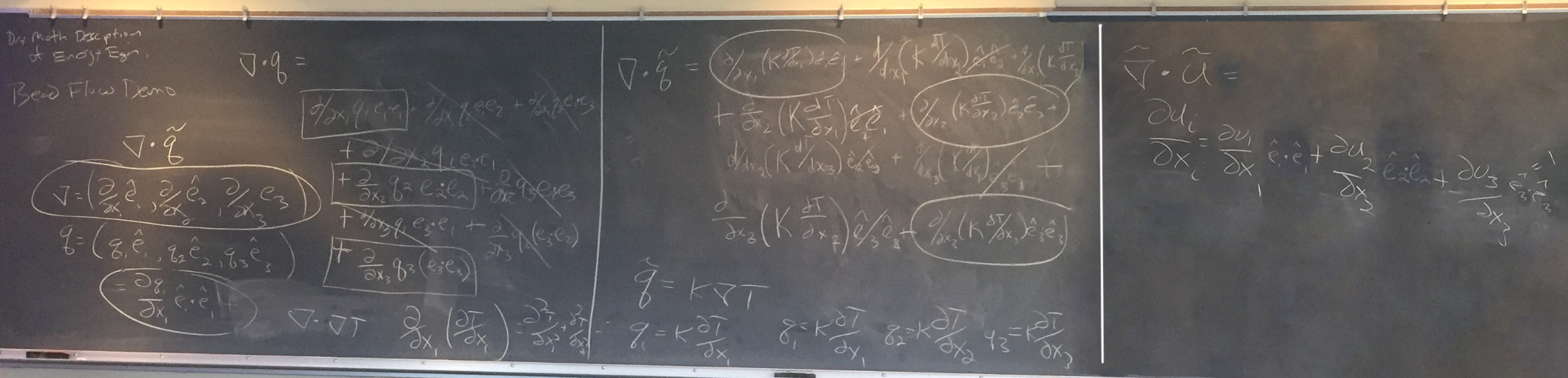
He reminded us to continue to do them long-hand with cancelations until the process feels ingrained enough.
With the energy equations in mind, Chris did another exercise representing lessons from rolling ball demo in physical ocean. Students in teams of four were asked to use plastic piping to represent the flow of heat at the locations in a watershed (Team West's locations shown in purple):

Students found the location based on the dimensions of the classroom and oriented the piping:

Students were asked to answer three questions at each location:
1. How to represent each location in terms of L1 and L2?
2. Is the gradient increasing (+) or decreasing (-) in the directions of L1 (E) and L2 (N)
3. What is the rough magnitude of the heat flow at those locations
Team West provided the answers at the front blackboard:

Students were then asked to quantify the heat flow in terms of a parcel diagrammed as such:

After students worked for ten minutes, Chris provided a relevant equation on the blackboard for students to contemplate:
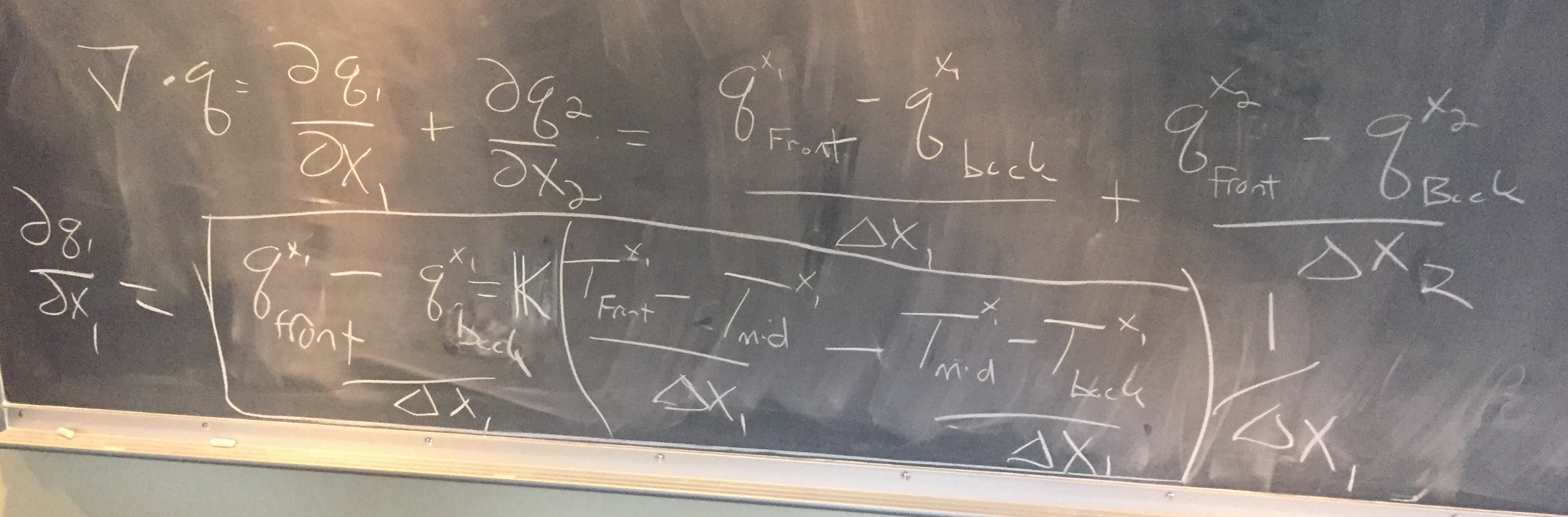
The term front refers to the parcel out front (more east or north) while the term back refers to the parcel behind (more west or south).
The calculations from the above blackboard equations expand as:
1. front/back q1:
front: (.001 cm2/second * -.5 °C /1 cm) = -.005 cm °C/second
back: (.001 cm2/second * -1 °C /1 cm) = -.01 cm °C/second
2. front/back q2:
front: (.001 cm2/second * -.5 °C /1 cm) = -.005 cm °C/second
back: (.001 cm2/second * -1 °C /1 cm) = -.01 cm °C/second
3. ▽ · q:
(-.005 - -.01) + (-.005 - -.01) + 0 = .01 cm °C/second
(just doing flow at the surface so no third term q3)
Chris suggested students ponder on this all weekend until it becomes more familiar and anticipated.

