Class on February 8 2019
Chris started by writing out equations for the conservation of mass (first), the conservation of momentum (second), and conservation of energy (third)
and suggested there were ways to remember how to write them by studying the pieces:
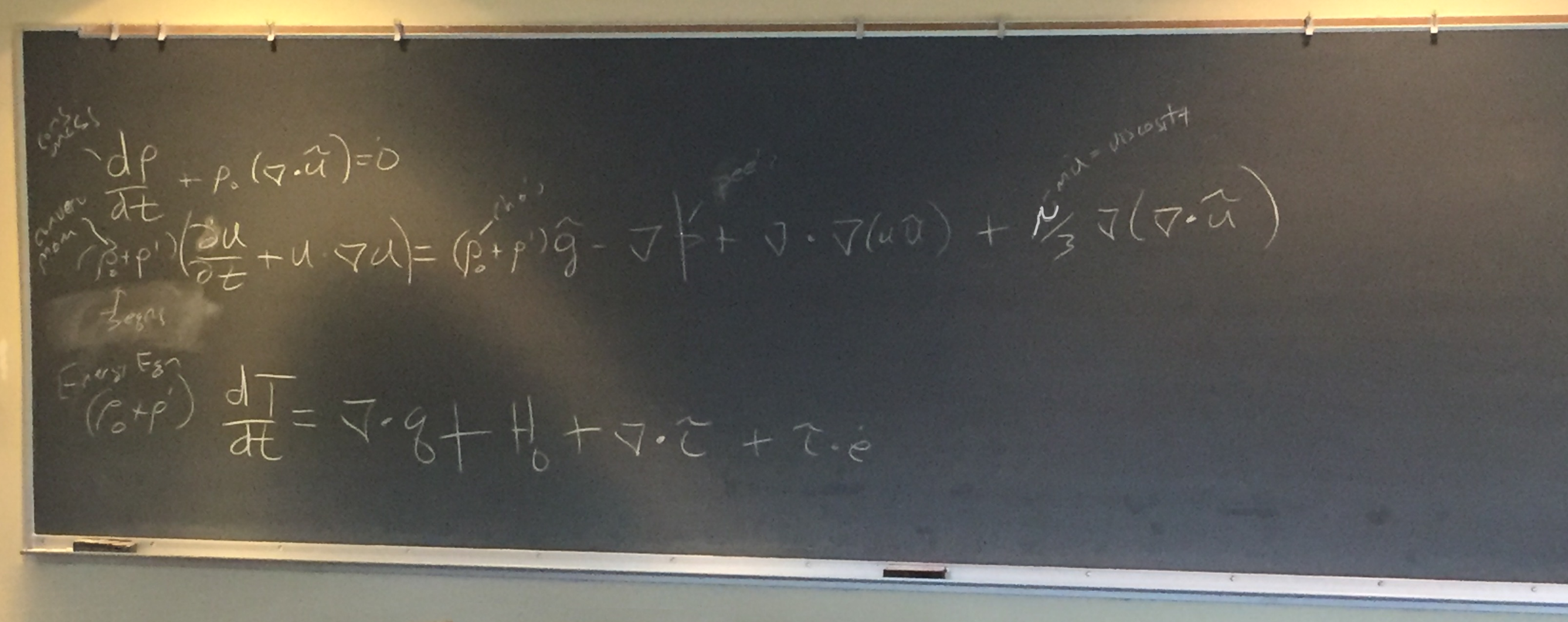
Chris reviewed two types of notation:
1. indicial notation (e.g. Ai)
2. vector notation (e.g. using ▽ and ~) — used more often in journals and publications
Chris showed the vector notation expansion of the conservation of momentum on the blackgboard (above).
The class focused on the Energy equation (the third equation on the board), starting by looking at the time change in temperature following a parcel of water.
We started by considering the heat flux component: ▽ . q
Chris worked with a research partner who consistently spilled his coffee when pursuing data gathering from a Acoustic Doppler Current Profiler (ADCP) that is typical for measuring currents. It's a good idea to keep the ADCP in place for a full tidal cycle (12+ hours) to be able to smooth out the effect of the tide on the current.
Chris showed an example of evaluating 3D temperature data collection using foam to visualize a 3-D gradient:

Chris led a physical exercise to gain insight into heat flow (Fourier's Law of Heat Flow)
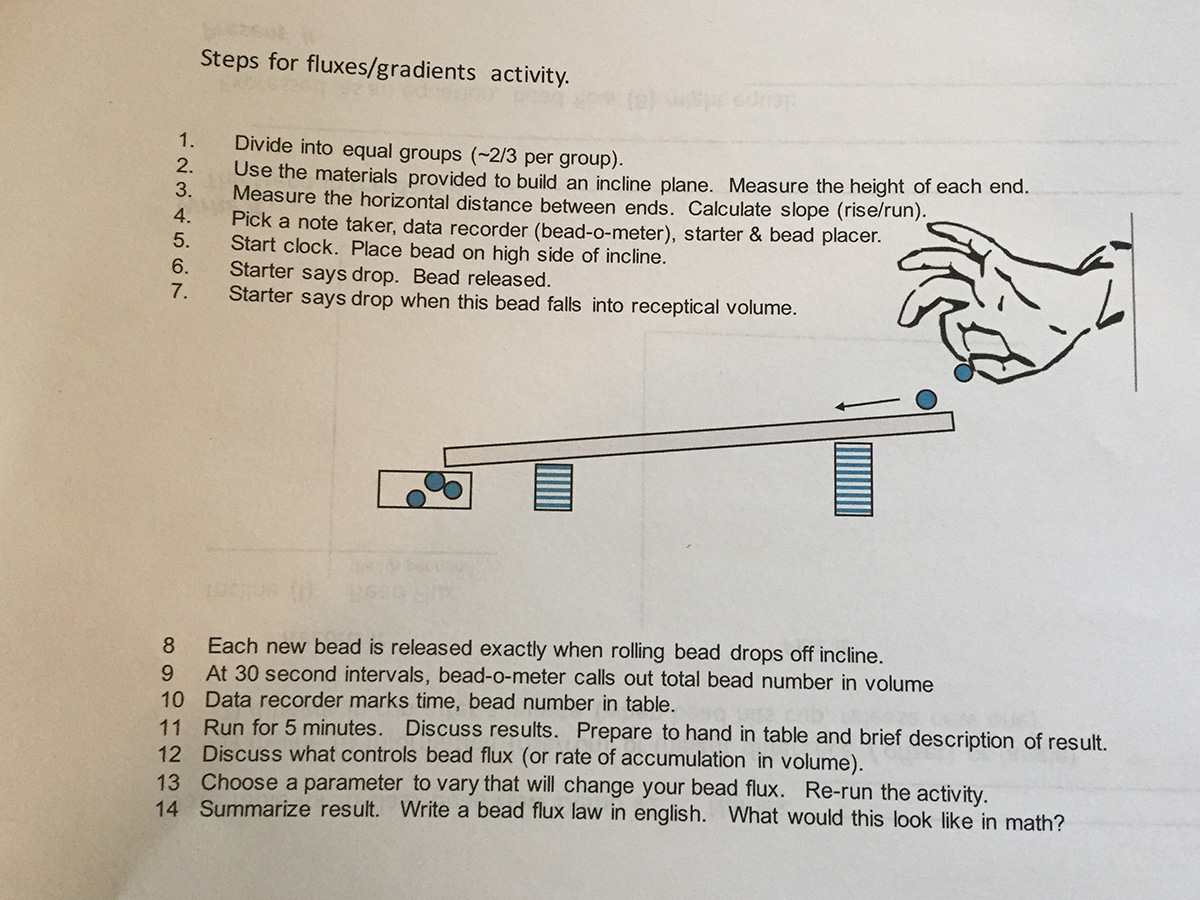
which looked like:

One example of flux of rolling balls on a slope:
the x1 distance was 74 centimeters
the x2 distance was 0 centimeters
the h distance was 8 centimeters
dh/dx1 = 8/74

Students found that as the gradient increases, the simulated heat flow increases
things that could change the result:
1. ball size
2. ball weight
3. friction (texture of wood or bead)
Students created an equation: BF = 1/R * ▽ h * A
BF - bead flow
R - roughness
h - height
A - area
Students, in teams, were asked to derive a heat flow equation from the bead flow exercise:
q = K * A * ▽ T
q = -k * ▽ T
q is local heat flux density (W/m2)
k is the materials conductivity (W/m/K)
▽ T is the temperature gradient (K/m)
Students were given homework assignment 3 to work on over the weekend. We would continue working on the Energy equation the next class time.
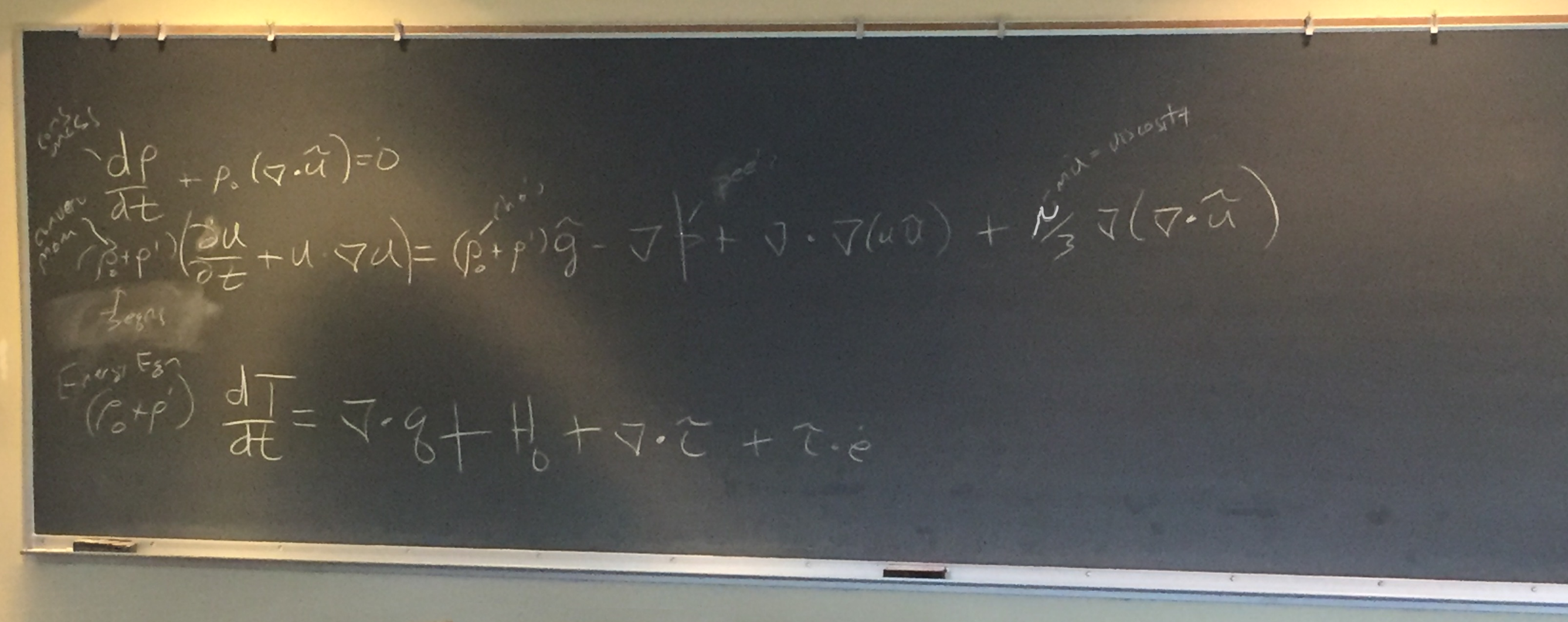
Chris reviewed two types of notation:
1. indicial notation (e.g. Ai)
2. vector notation (e.g. using ▽ and ~) — used more often in journals and publications
Chris showed the vector notation expansion of the conservation of momentum on the blackgboard (above).
The class focused on the Energy equation (the third equation on the board), starting by looking at the time change in temperature following a parcel of water.
We started by considering the heat flux component: ▽ . q
Chris worked with a research partner who consistently spilled his coffee when pursuing data gathering from a Acoustic Doppler Current Profiler (ADCP) that is typical for measuring currents. It's a good idea to keep the ADCP in place for a full tidal cycle (12+ hours) to be able to smooth out the effect of the tide on the current.
Chris showed an example of evaluating 3D temperature data collection using foam to visualize a 3-D gradient:

Chris led a physical exercise to gain insight into heat flow (Fourier's Law of Heat Flow)

which looked like:

One example of flux of rolling balls on a slope:
the x1 distance was 74 centimeters
the x2 distance was 0 centimeters
the h distance was 8 centimeters
dh/dx1 = 8/74

Students found that as the gradient increases, the simulated heat flow increases
things that could change the result:
1. ball size
2. ball weight
3. friction (texture of wood or bead)
Students created an equation: BF = 1/R * ▽ h * A
BF - bead flow
R - roughness
h - height
A - area
Students, in teams, were asked to derive a heat flow equation from the bead flow exercise:
q = K * A * ▽ T
q = -k * ▽ T
q is local heat flux density (W/m2)
k is the materials conductivity (W/m/K)
▽ T is the temperature gradient (K/m)
Students were given homework assignment 3 to work on over the weekend. We would continue working on the Energy equation the next class time.

