Class on February 1 2019
Students turned in their first of six code-based homework sets required of the course. An example of the assignment is available as a Python Notebook
that can be run with Jupyter notebook software (right mouse-click and choose Save Link As to maintain the notebook syntax).
Chris continued the mathematical discussion to prepare students for upcoming activities in the class.
For the purpose of the class math, a vector was defined as a ordered triple (unchanged by coordinate axes):
x1 is the axes coming towards you
x2 is the traditional x direction
x3 is the traditional y direction
Useful operations between vectors include A.B (dot product) and AxB (cross product),
Chris demonstrated the significance of the dot product result via a chair and ropes example (below) (how do vectors pull together? cross product - the normal force from both vectors)

The dot product can be demonstrated as the magnitude of a shadow cast by one vector on the unit vector of the other.
The cross product provides the effective magnitude and direction of force (as a vector) provided by the pull of one of the two vectors on the other.
The cross product, in fact, provides a vector as a result of the computation:
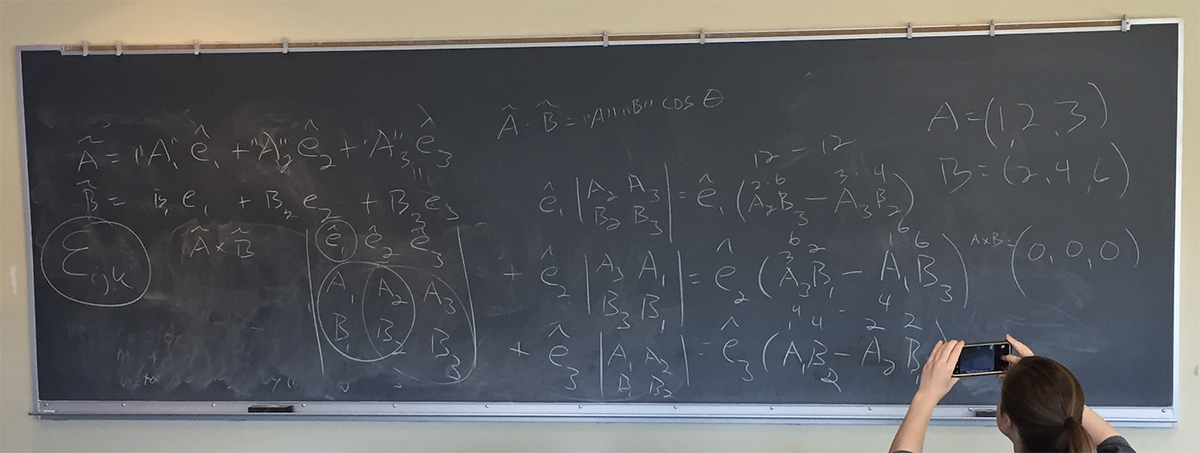
Chris then turned attention to Derivatives and Differentials:
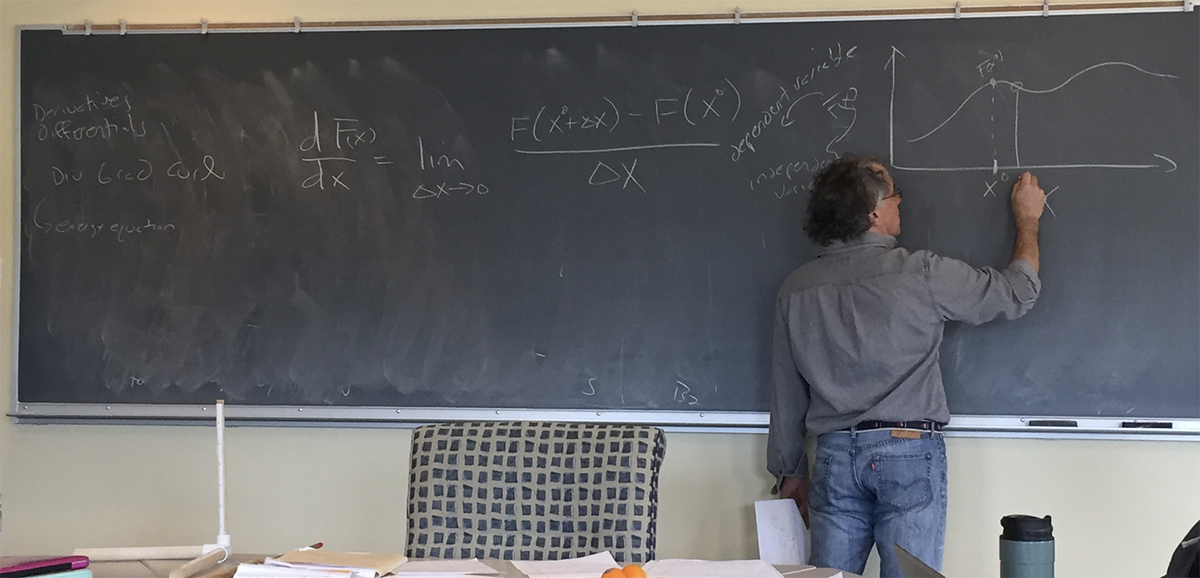
Chris then demonstrated a visual significance of a tangent plane to use the axes to find the derivative as a plane:

which results in the formula highlighted by a red border here:
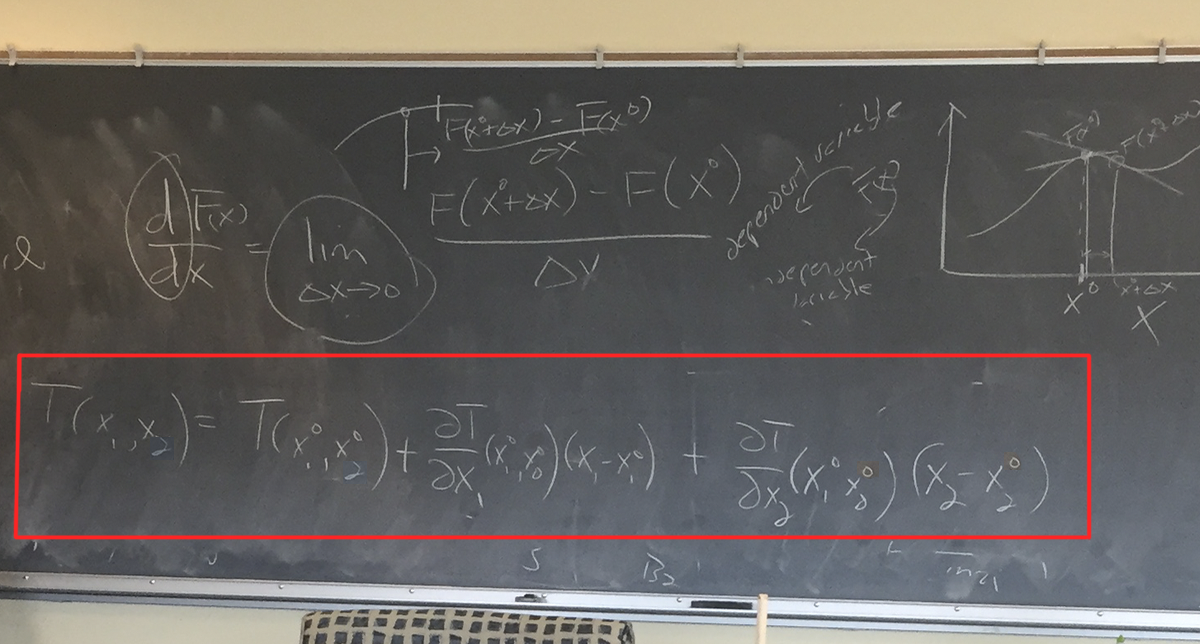
Chris handed out another homework assignment which would be continued in class on Monday. Students were reminded they can contact Bruce with any Python or MATLAB questions after they have attempted to research the answer in earnest long enough.
Chris continued the mathematical discussion to prepare students for upcoming activities in the class.
For the purpose of the class math, a vector was defined as a ordered triple (unchanged by coordinate axes):
x1 is the axes coming towards you
x2 is the traditional x direction
x3 is the traditional y direction
Useful operations between vectors include A.B (dot product) and AxB (cross product),
Chris demonstrated the significance of the dot product result via a chair and ropes example (below) (how do vectors pull together? cross product - the normal force from both vectors)
A = ||A1|| * e1 + ||A2|| * e2 + ||A3|| * e3 B = ||B1|| * e1 + ||B2|| * e2 + ||B3|| * e3 A.B = ||A|| * ||B|| * cos(angle between them) <--adjacent/hypotheneuse A.B = A1*B1*e1.e1 + A1*B2*e1.e2 + A1*B3*e1.e3 + A2*B1*e2.e1 + A2*B2*e2.e2 + A2*B3*e2.e3 + A3*B1*e3.e1 + A3*B2.e3.e2 + A3*B3.e3.e3 Using cosine, the e#.e# terms reduce to: A.B = 1 0 0 0 1 0 0 0 1 And therefore reduces to: A.B = A1*B1*e1.e1 + A2*B2*e2.e2 + A3*B3*e3.e3

The dot product can be demonstrated as the magnitude of a shadow cast by one vector on the unit vector of the other.
The cross product provides the effective magnitude and direction of force (as a vector) provided by the pull of one of the two vectors on the other.
The cross product, in fact, provides a vector as a result of the computation:
AxB = ||A|| * ||B|| * sin(angle between them) <--opposite/hypotheneuse
AxB = e1 e2 e3
A1 A2 A3
B1 B2 B3
the cross product is the determinant:
AxB = e1 |A2 A3| + e2 |A3 A1| + e3 |A1 A2|
|B2 B3| |B3 B1| |B1 B3|
which, when expanded results in:
AxB = e1*(A2*B2 - A3*B2) + e2*(A3*B1 - A1*B3) + e3(A1*B2 - A2*B1)
examples: [1,2,3] x [2,4,6] = [0,0,0]
(no cross pull - no 'honest john')
[1,2,3] x [-2,-2,-2] = [-2,-8,6]
(much cross pull - 'significant honest john')
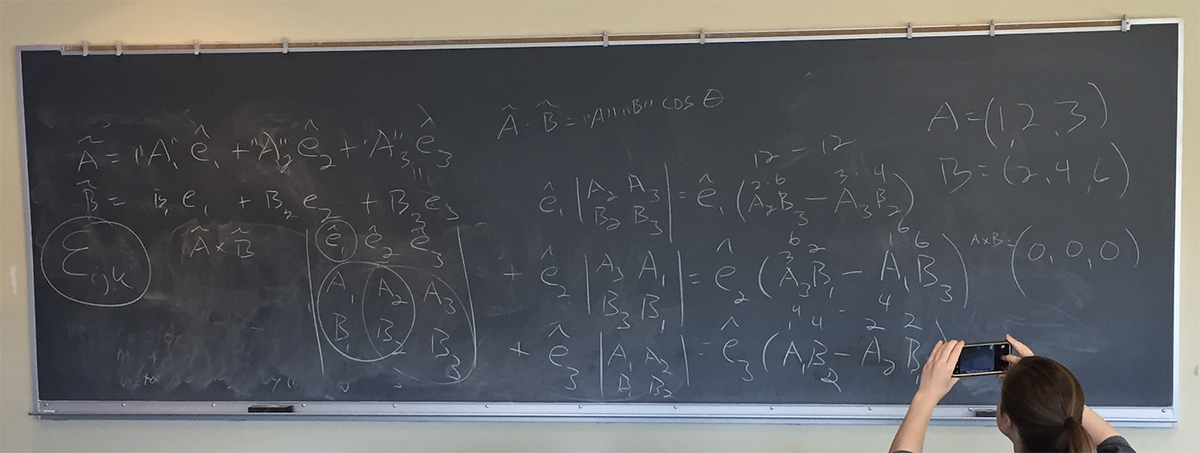
Chris then turned attention to Derivatives and Differentials:
dF(x) F(x0+dx) - F(x0) ----- = lim ---------------- gives you a slope dx dx->0 dx (you want the smallest dx near the point — where the slope is the tangent at that point)
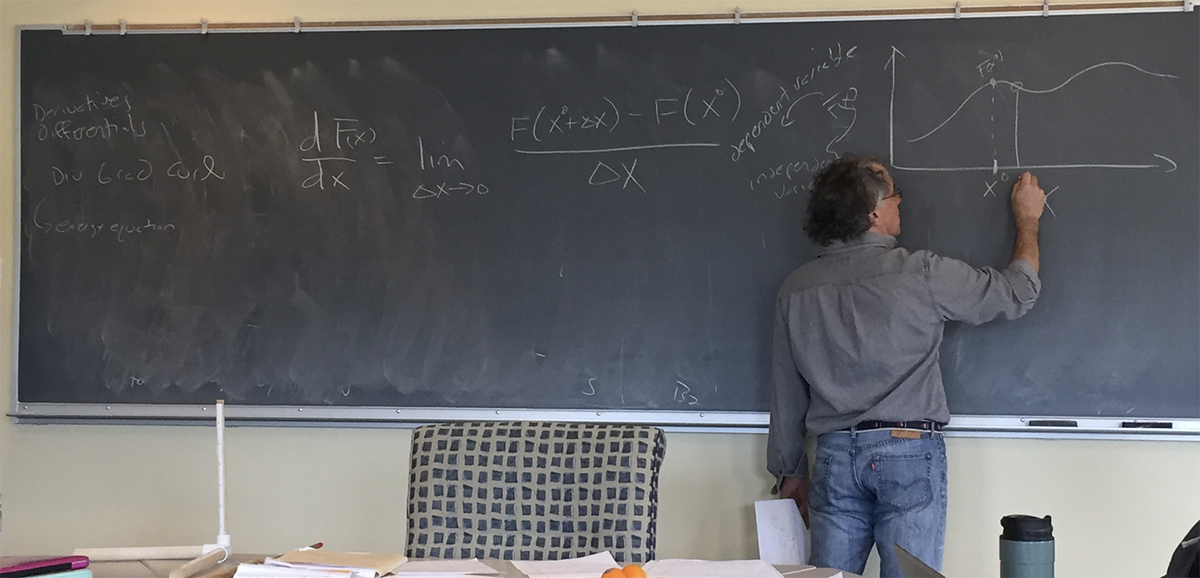
Chris then demonstrated a visual significance of a tangent plane to use the axes to find the derivative as a plane:

which results in the formula highlighted by a red border here:
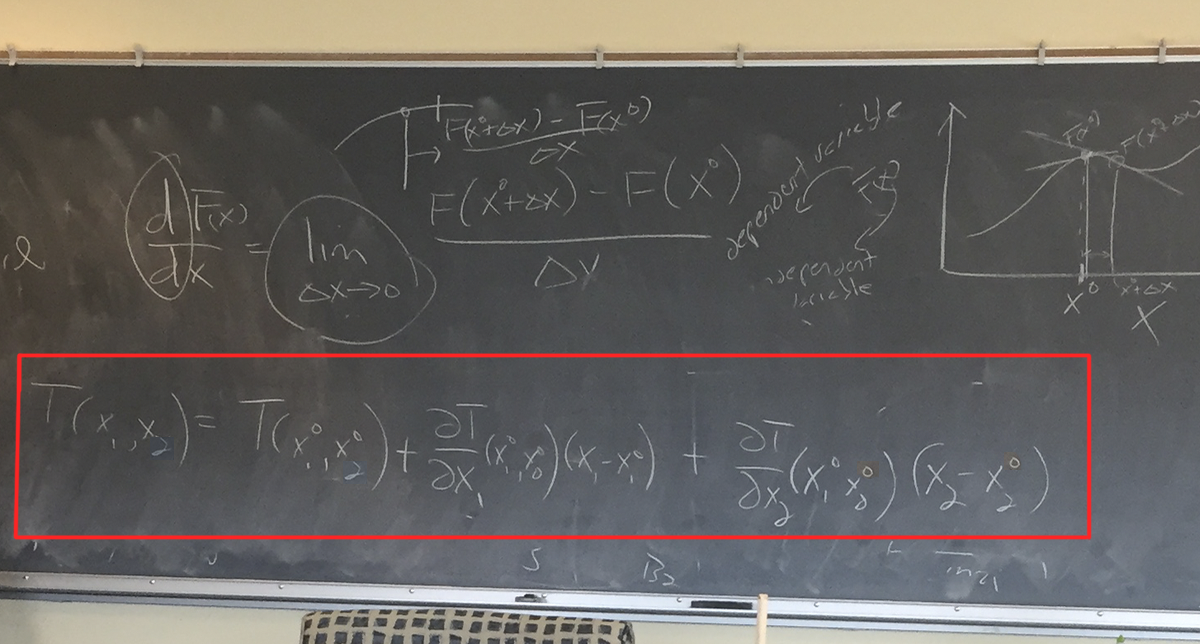
Chris handed out another homework assignment which would be continued in class on Monday. Students were reminded they can contact Bruce with any Python or MATLAB questions after they have attempted to research the answer in earnest long enough.

