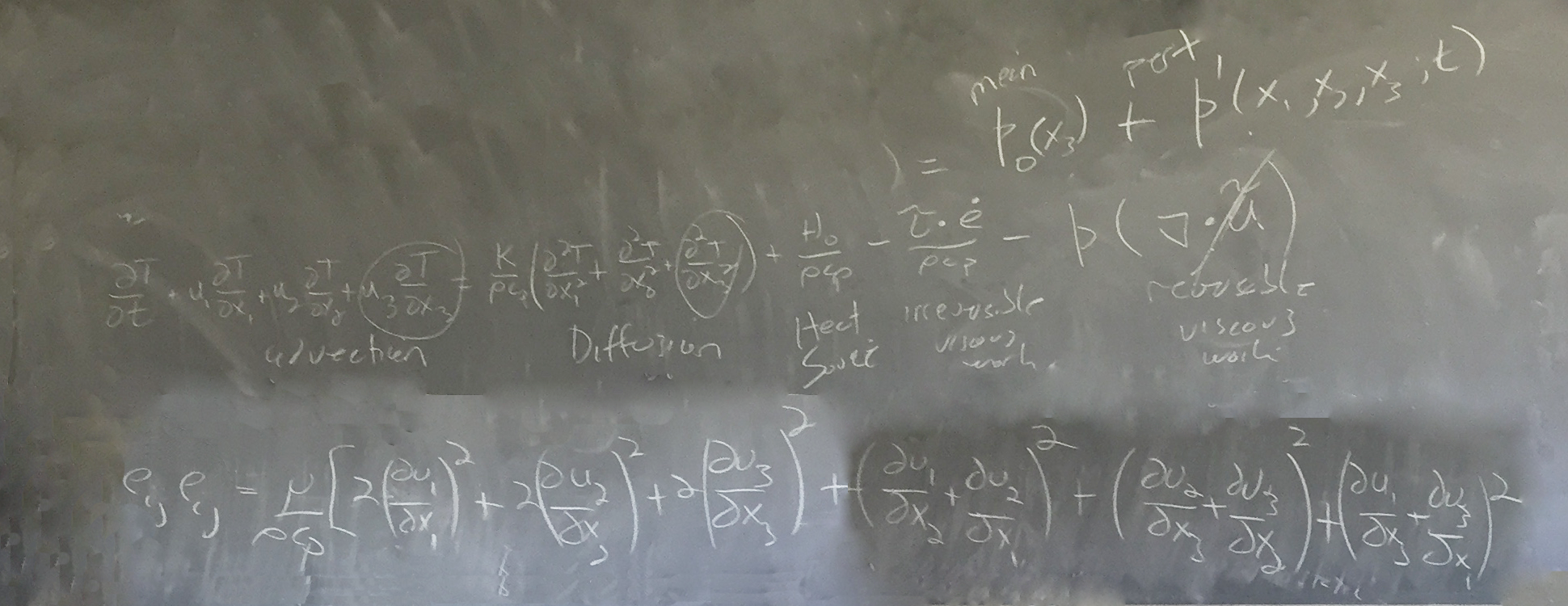Class on April 15 2019
Chris dedicated the class to building the final equation we would be using in class to calculate
hydrothermal dynamics. We started with where we left off last class, but with the conservation
of momentum equation for the i=3 component instead of i=2:
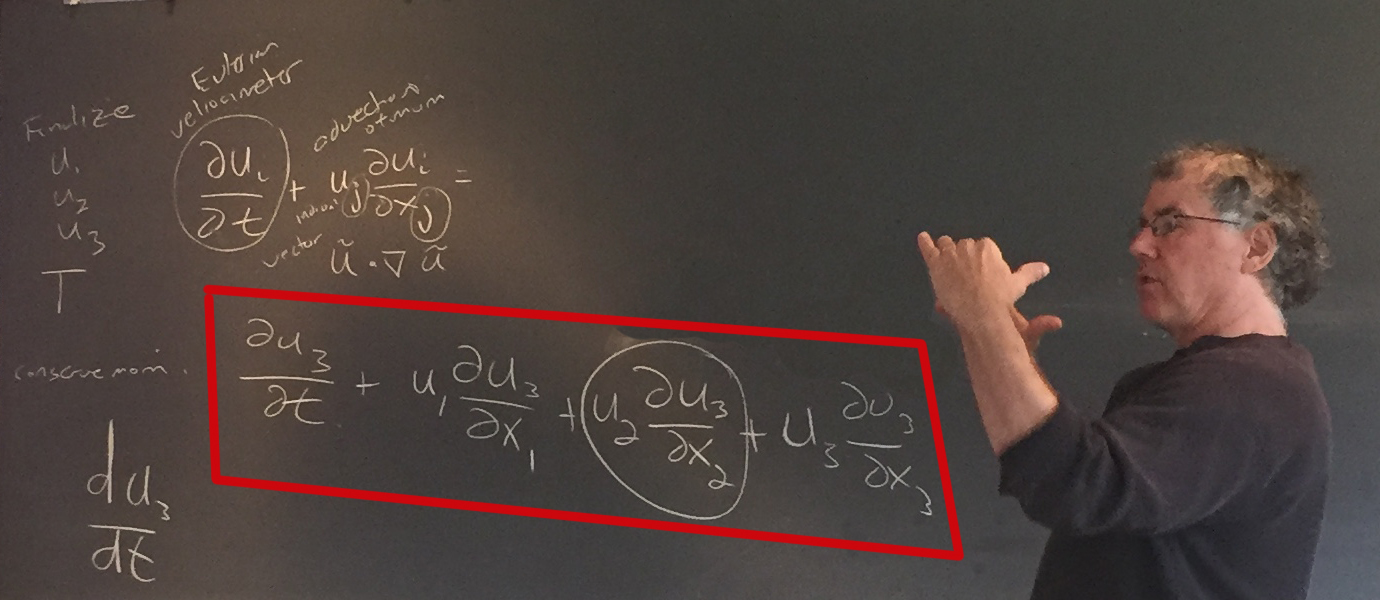
Chris then worked on an expansion of the equation:
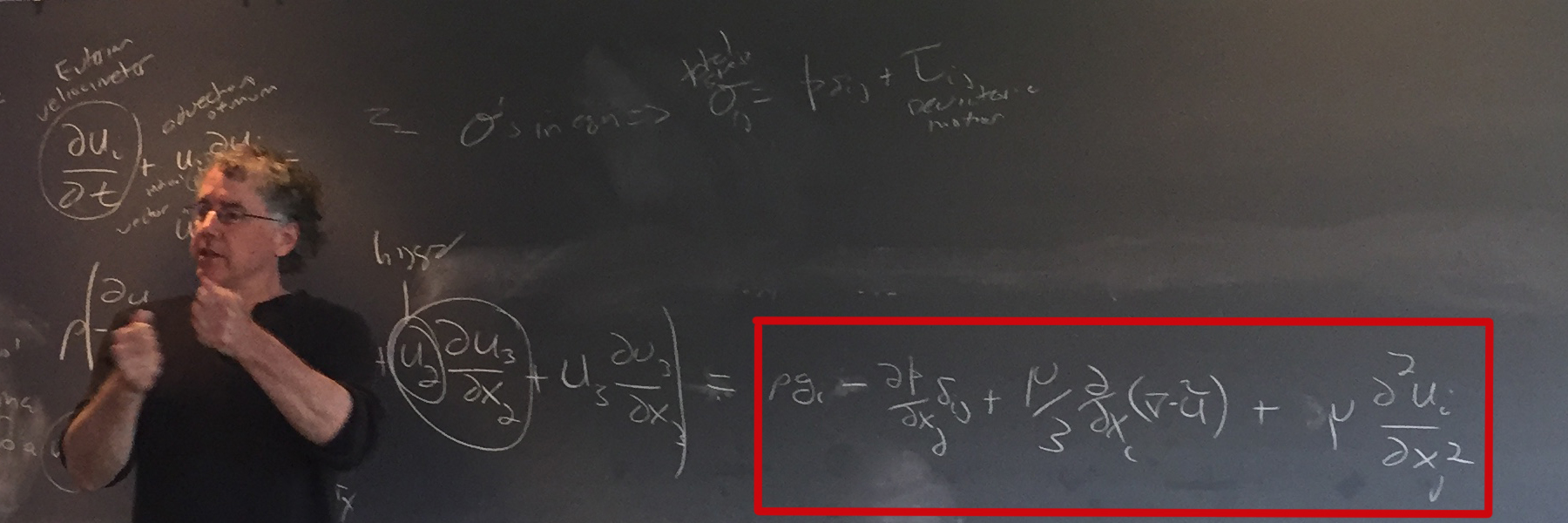
Chris reviewed the stress force (rho) as comprising of components:
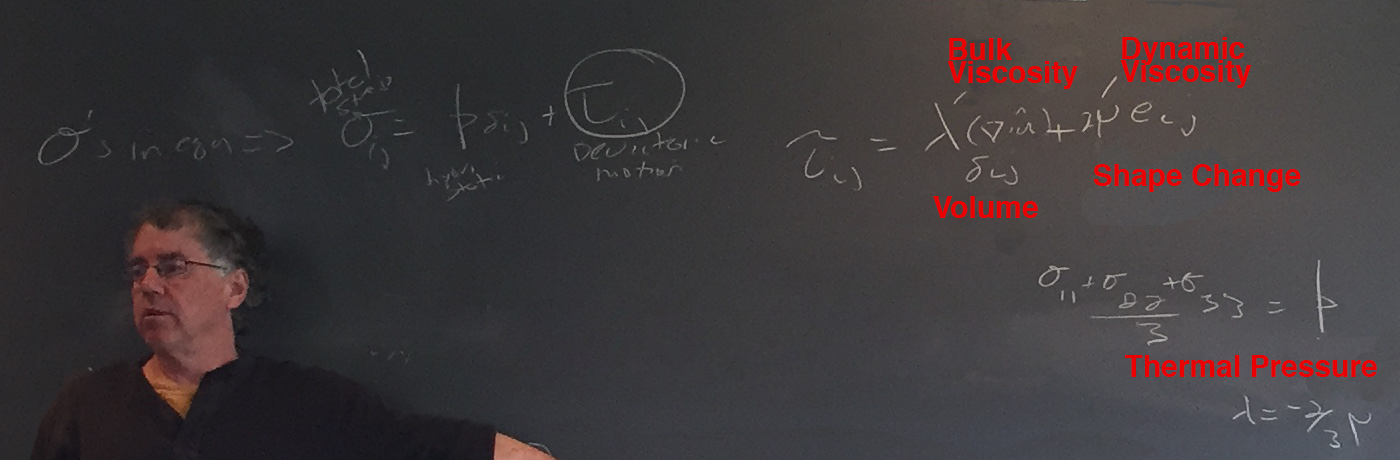
Chris then continued performing additional algebraic transformations to convert the conservation of momentum equation:

Chris then ran through a series of stress situations to consider u * (du1/dx2) as viscosity (u) and sheer (du1/dx2) effects and the combination of both to consider how much actual sheer takes place). If viscosity is low, the stress is minimal. When viscosity is high, the overall stress increases:
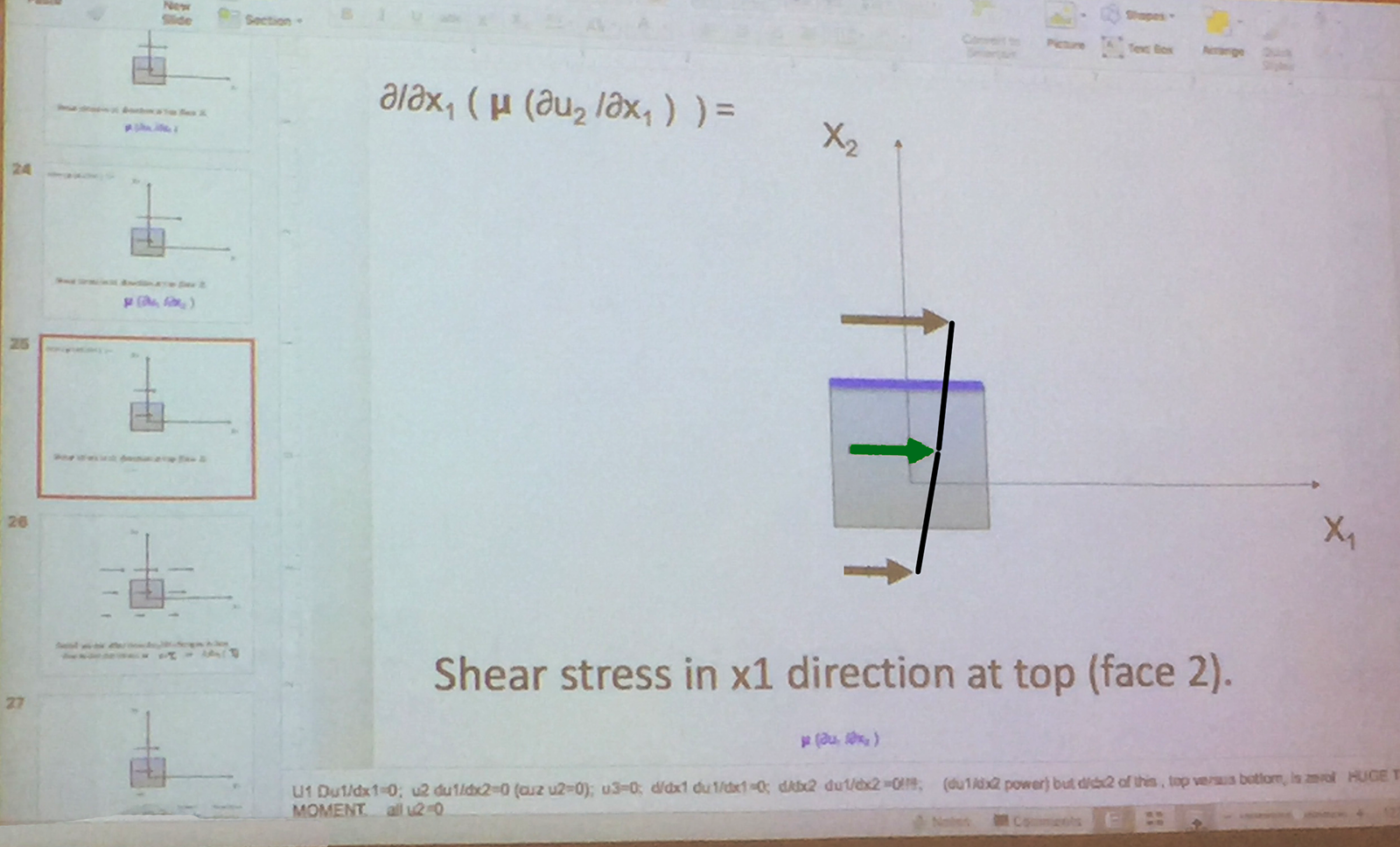
Chris reminded the students that if you only know the vector magnitude of one of the two neighbors, you don't know the effect of the parcel (the del operator needs to take all neighbors into account). Chris reminded students that "diffusion abhors curves" — but viscosity determines how fast the differences straightening out to linear.
Chris then asked the students to write out the conservation of momentum equation with terms they consider quintessential:
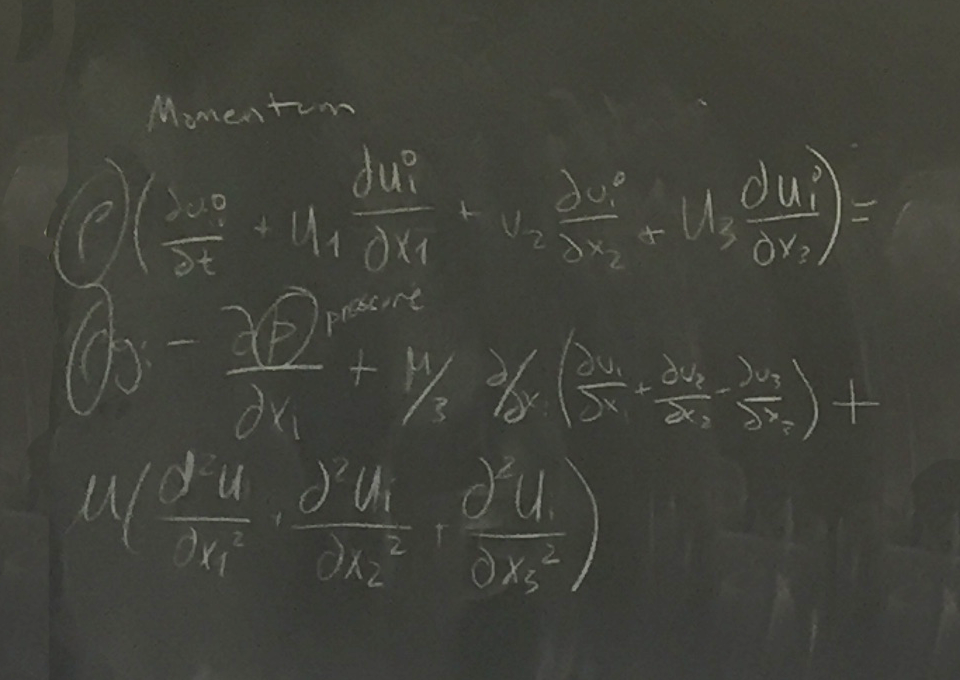
Chris then asked students to write out the stress force equation with terms they consider quintessential (which Chris then helped rearrange to more useful form):
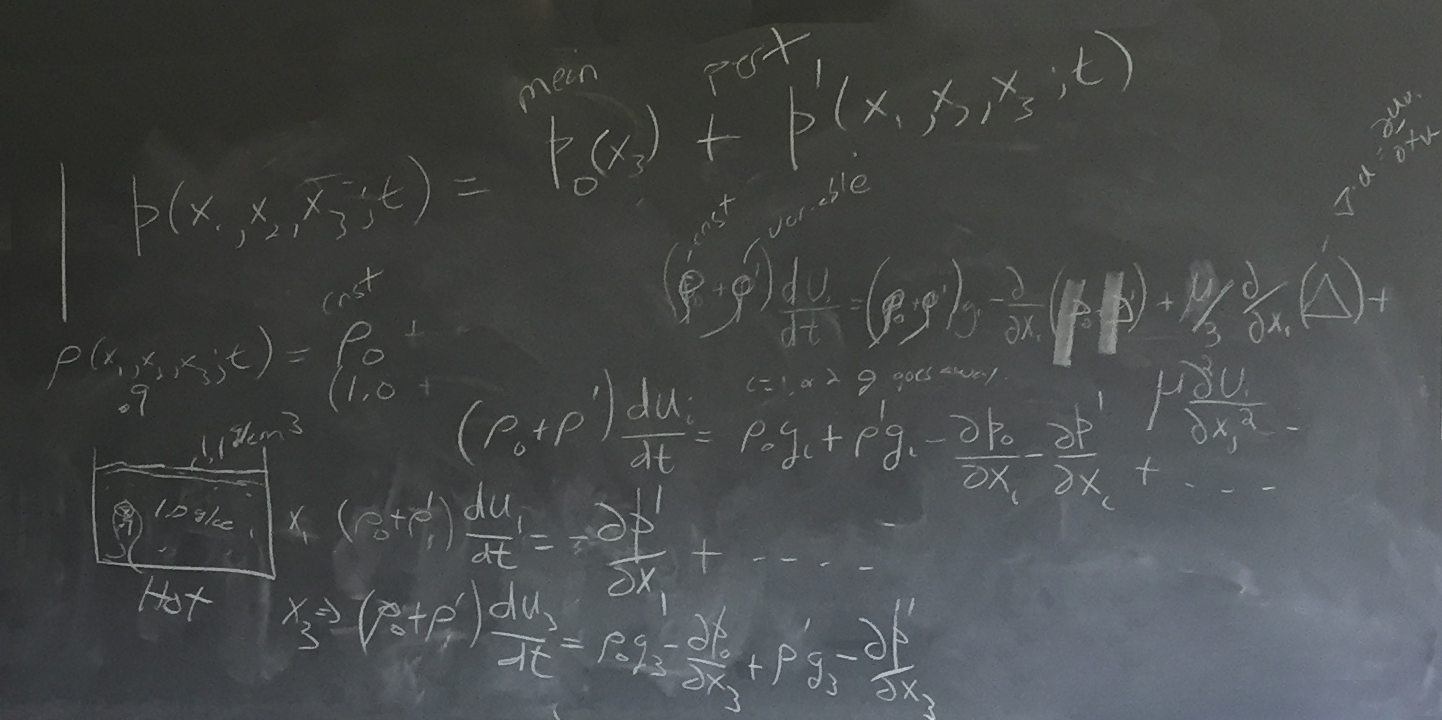
Chris reminded students that many of the terms are simplified by the assumption of an incompressable field (which is a reasonable assumption for the ocean):
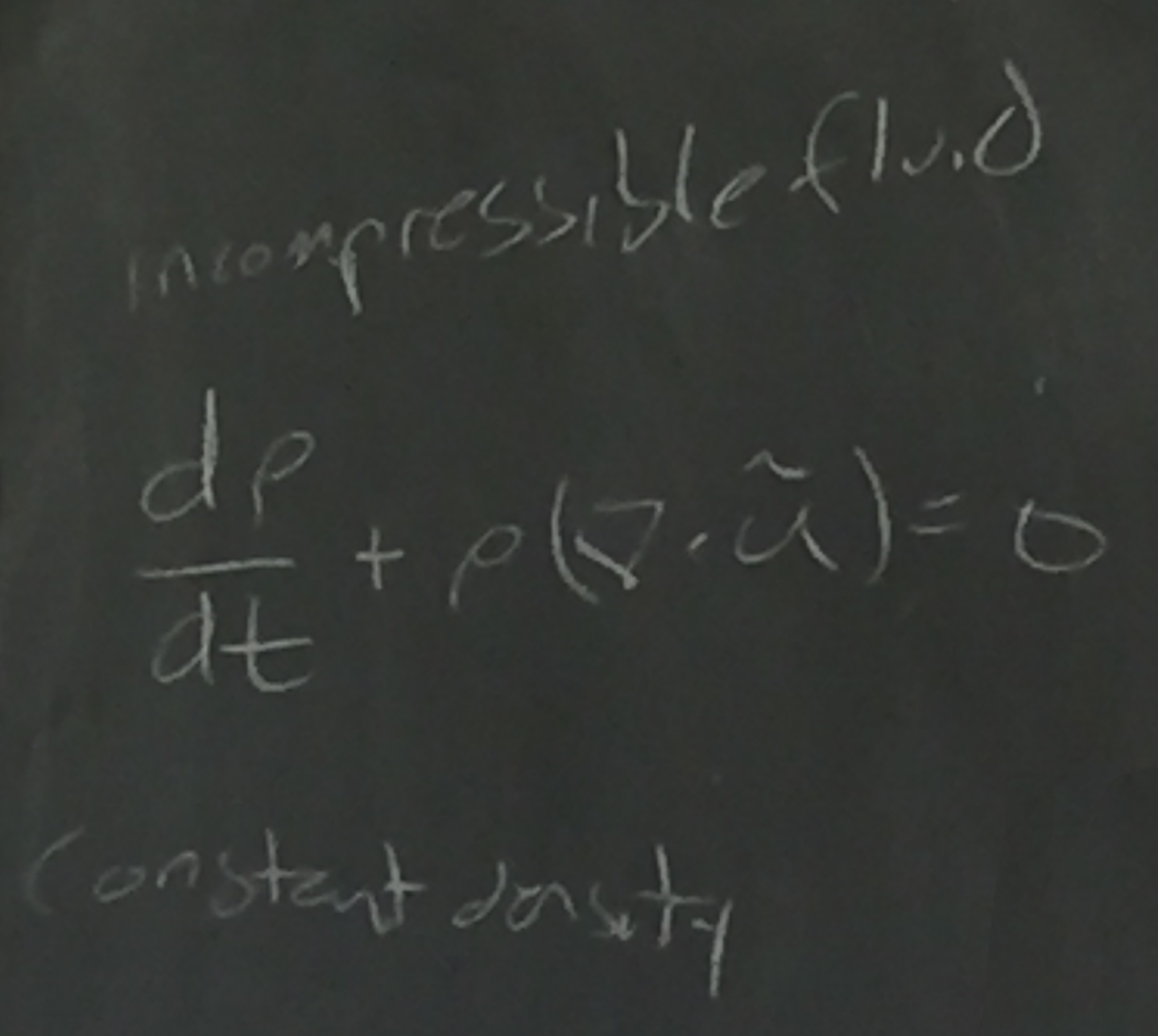
Chris finished the class by writing out the full hydrothermal dynamics equation:
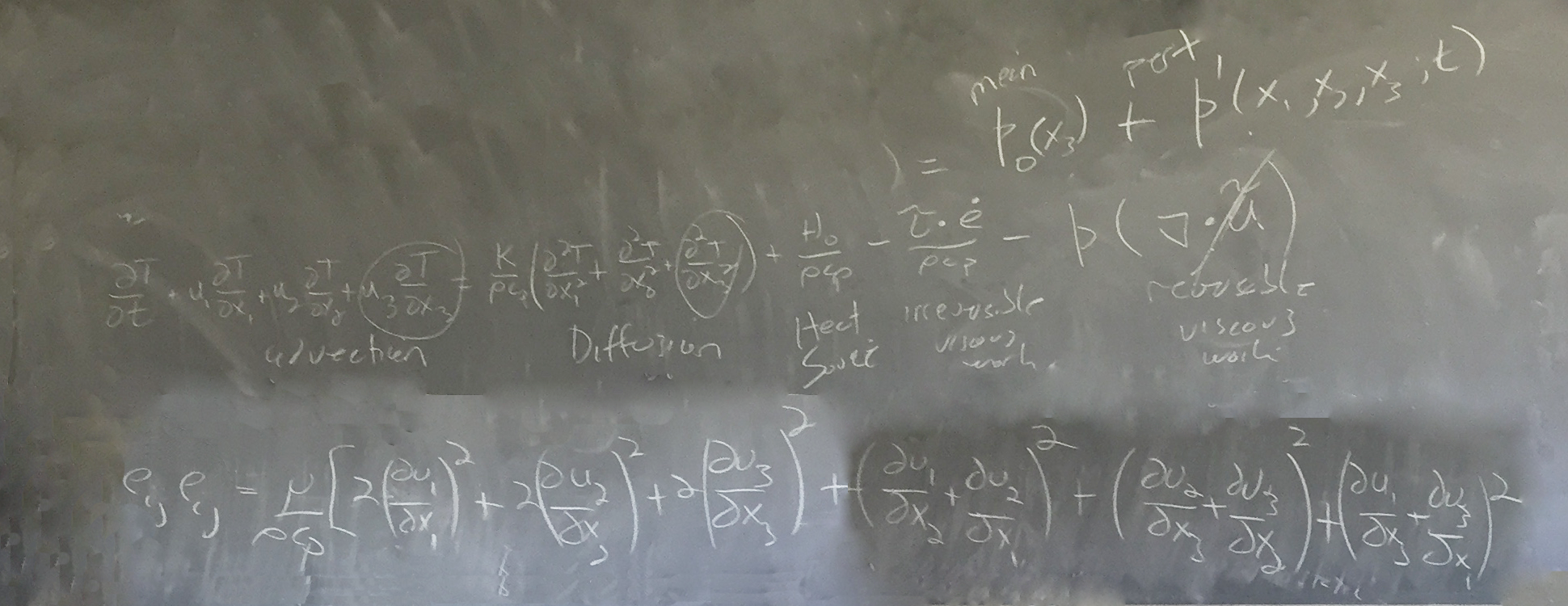
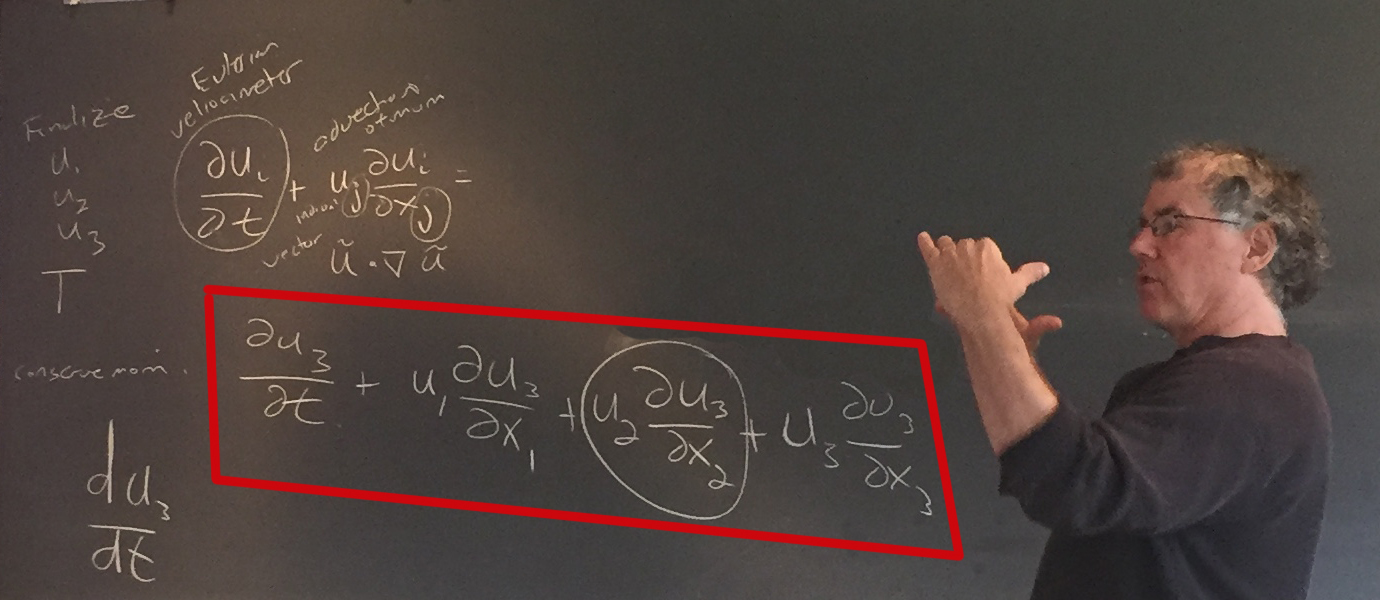
Chris then worked on an expansion of the equation:
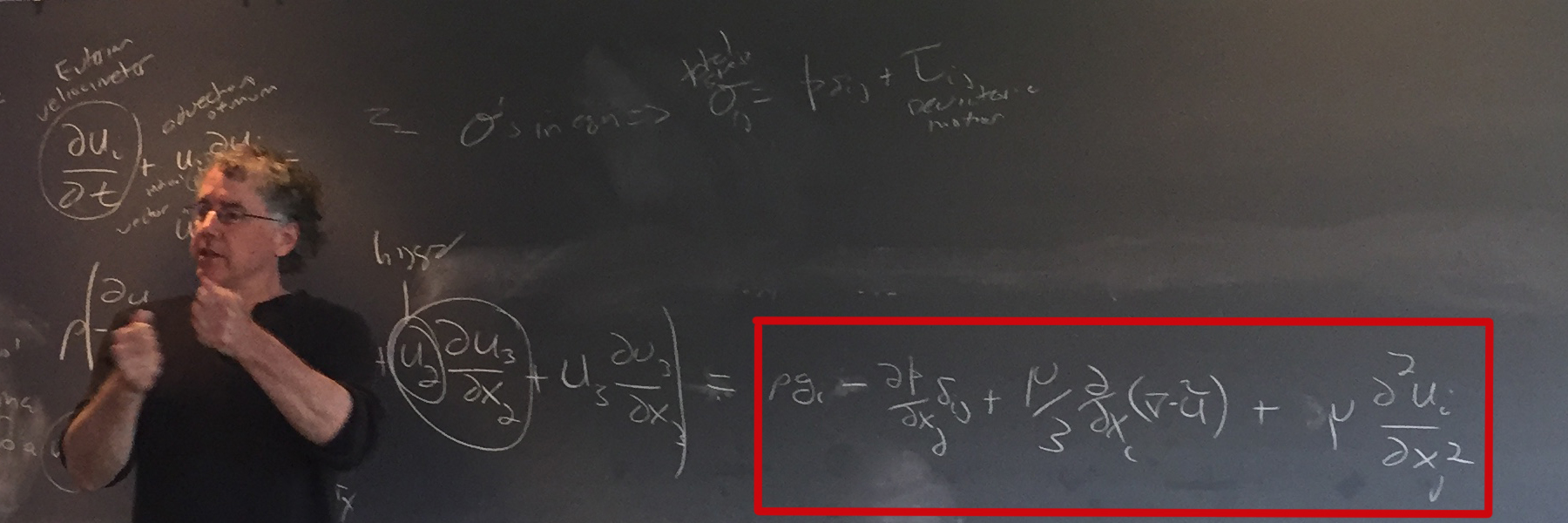
Chris reviewed the stress force (rho) as comprising of components:
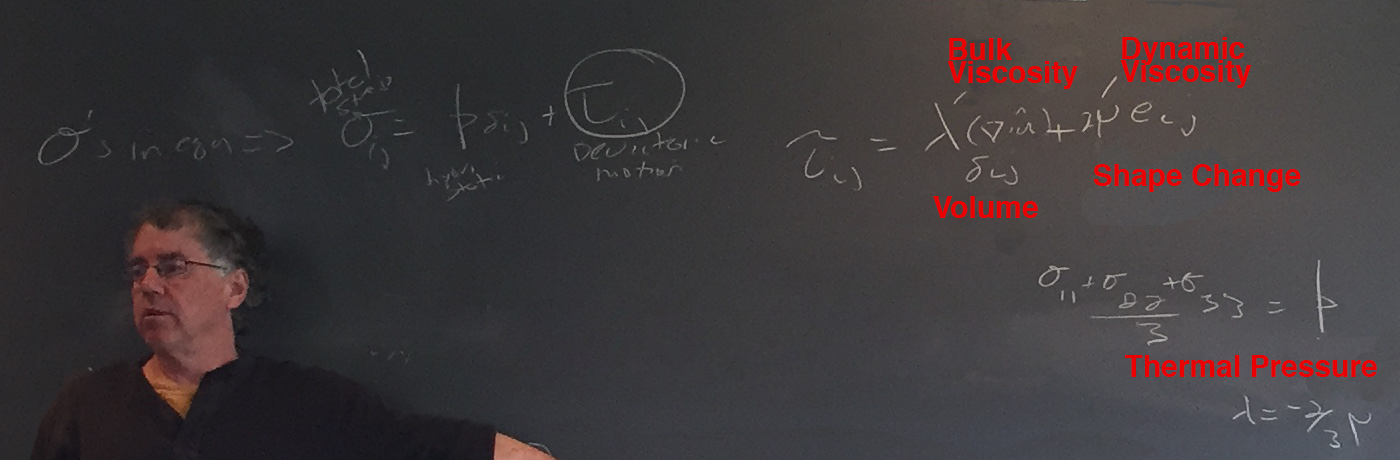
Chris then continued performing additional algebraic transformations to convert the conservation of momentum equation:

Chris then ran through a series of stress situations to consider u * (du1/dx2) as viscosity (u) and sheer (du1/dx2) effects and the combination of both to consider how much actual sheer takes place). If viscosity is low, the stress is minimal. When viscosity is high, the overall stress increases:

Chris reminded the students that if you only know the vector magnitude of one of the two neighbors, you don't know the effect of the parcel (the del operator needs to take all neighbors into account). Chris reminded students that "diffusion abhors curves" — but viscosity determines how fast the differences straightening out to linear.
Chris then asked the students to write out the conservation of momentum equation with terms they consider quintessential:
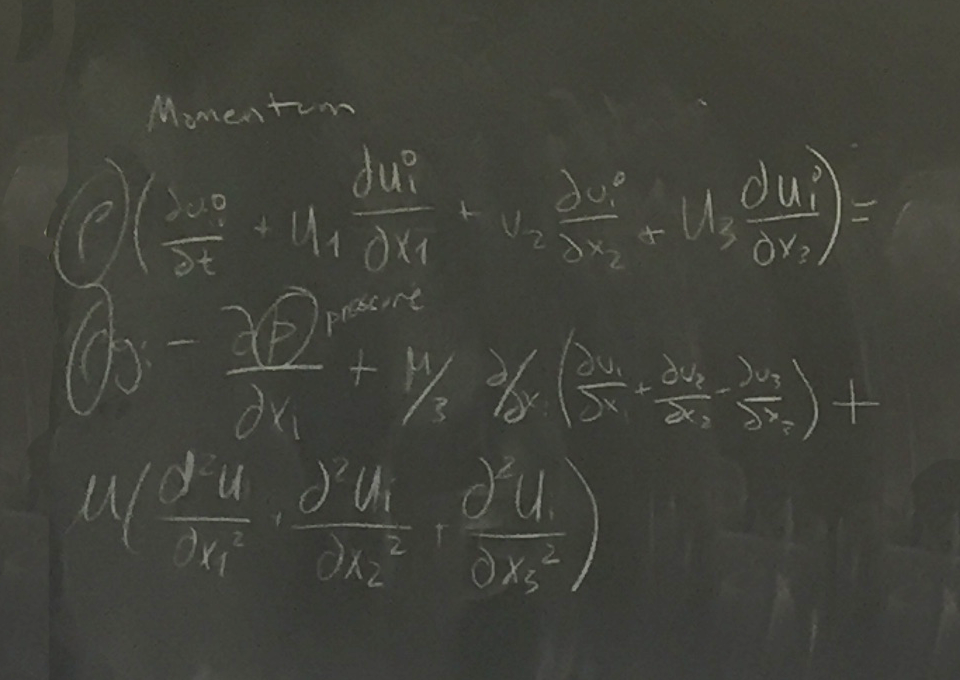
Chris then asked students to write out the stress force equation with terms they consider quintessential (which Chris then helped rearrange to more useful form):
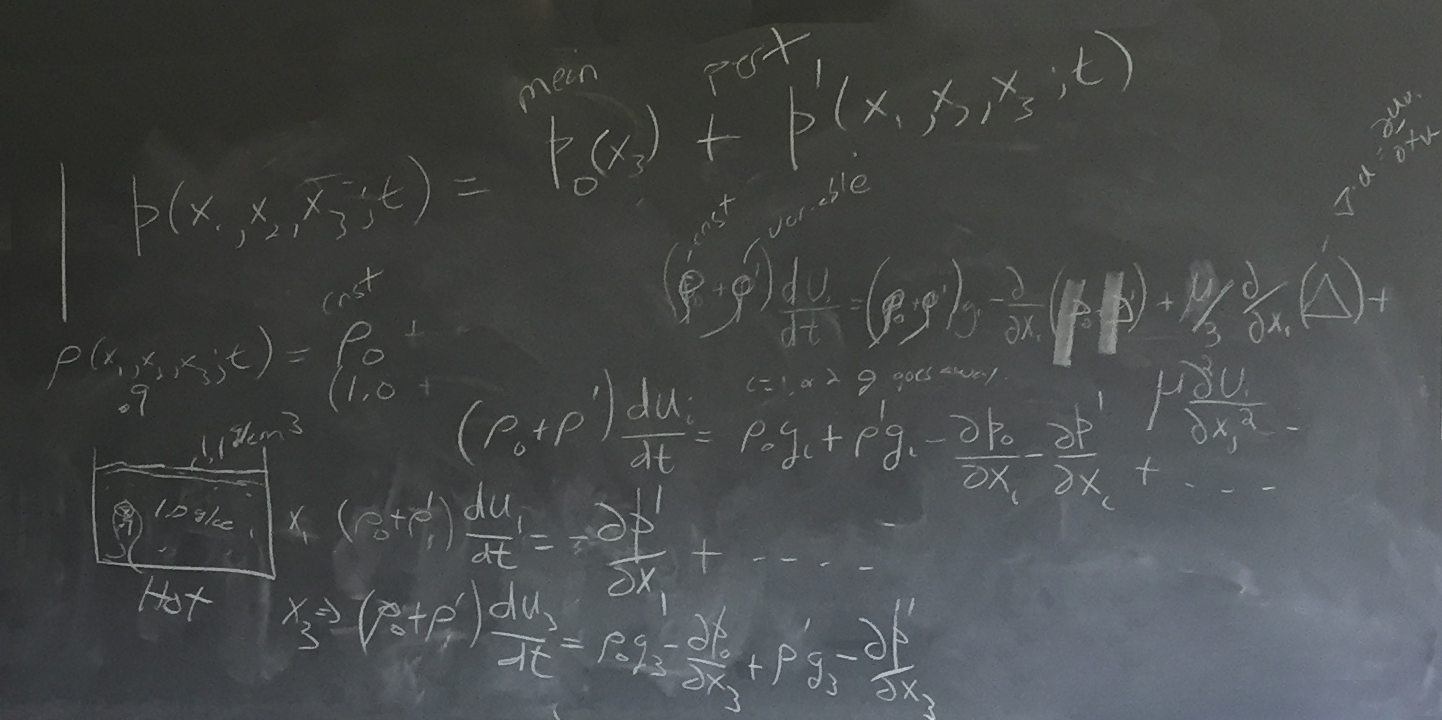
Chris reminded students that many of the terms are simplified by the assumption of an incompressable field (which is a reasonable assumption for the ocean):
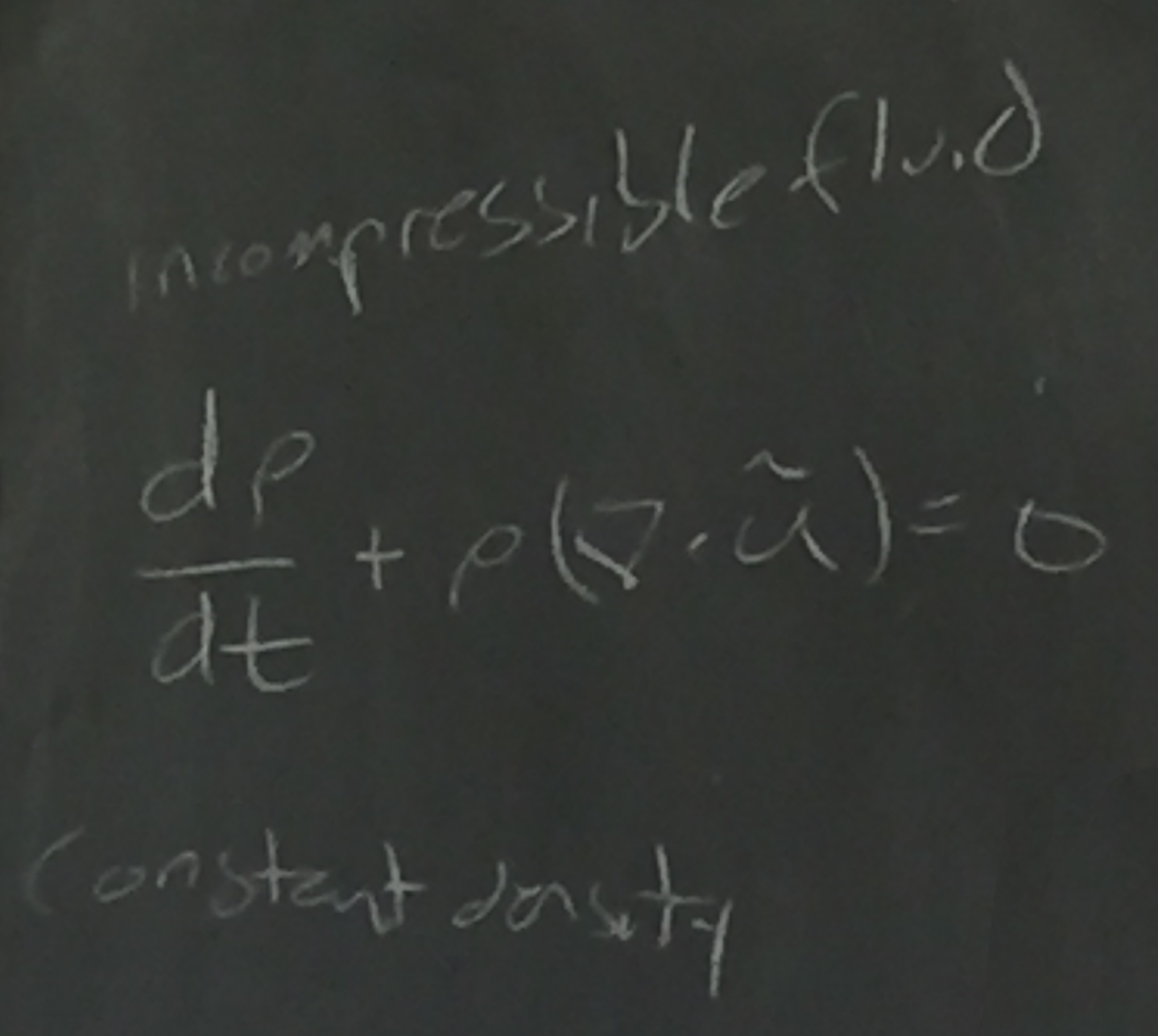
Chris finished the class by writing out the full hydrothermal dynamics equation: