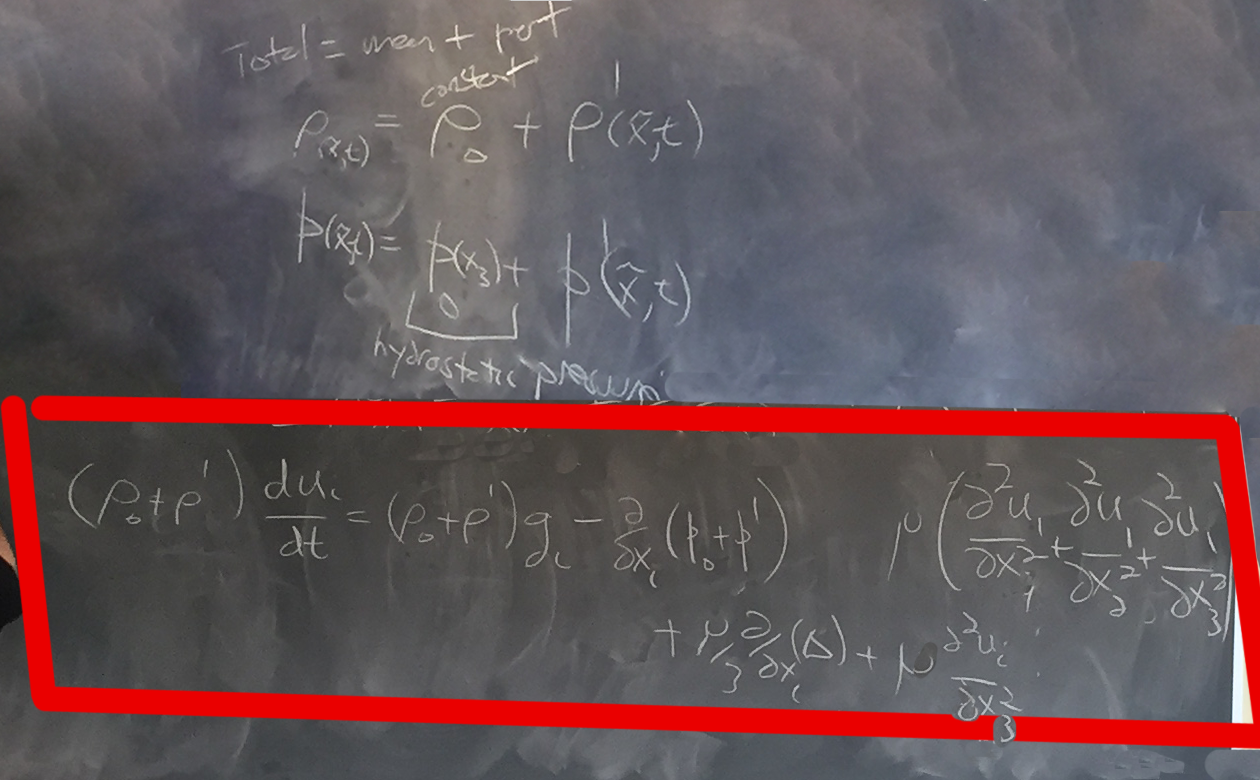Class on April 12 2019
Chris dedicated the class to building the momentum equations from pieces and through reductions
to get to a useful result for modeling purposes. He started with reviewing critical pieces, of
which Δ would be a key component in the final equation:
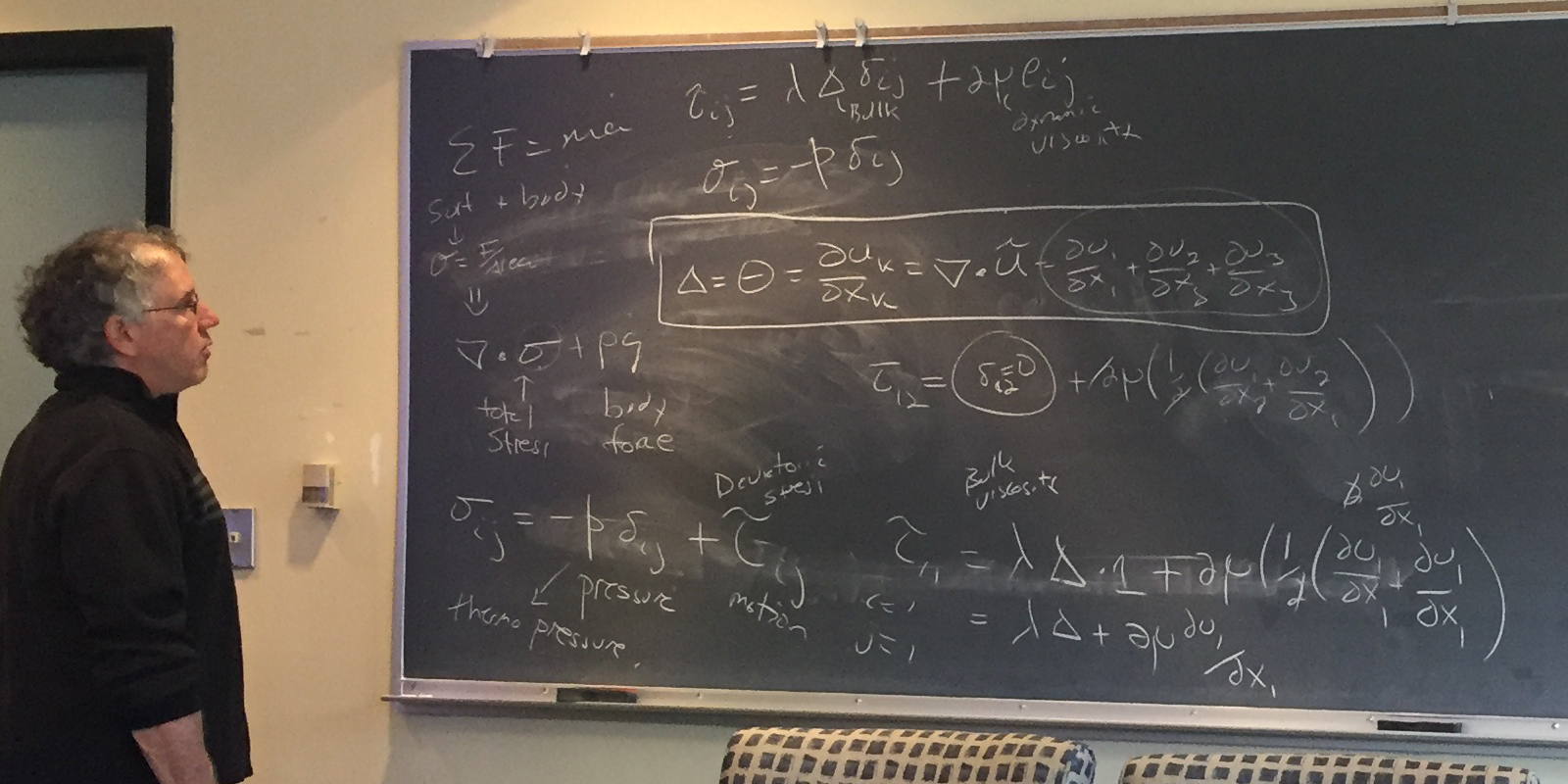
Chris then worked on the expansion of dui/dt:
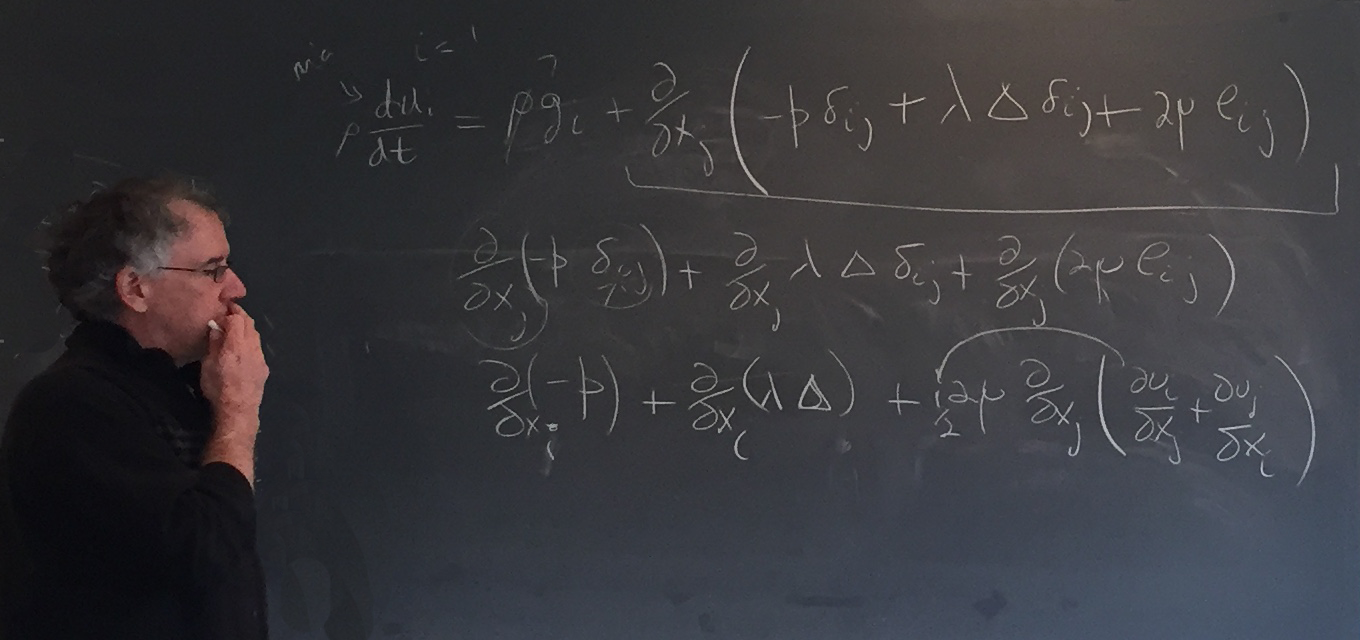
with the simplification of converting subscript j to i for a specific choice of axis (line 2 to 3 above).
Then, Chris pulled out some terms to prepare for simplifying the full momentum equation (line 3 to 4 below):
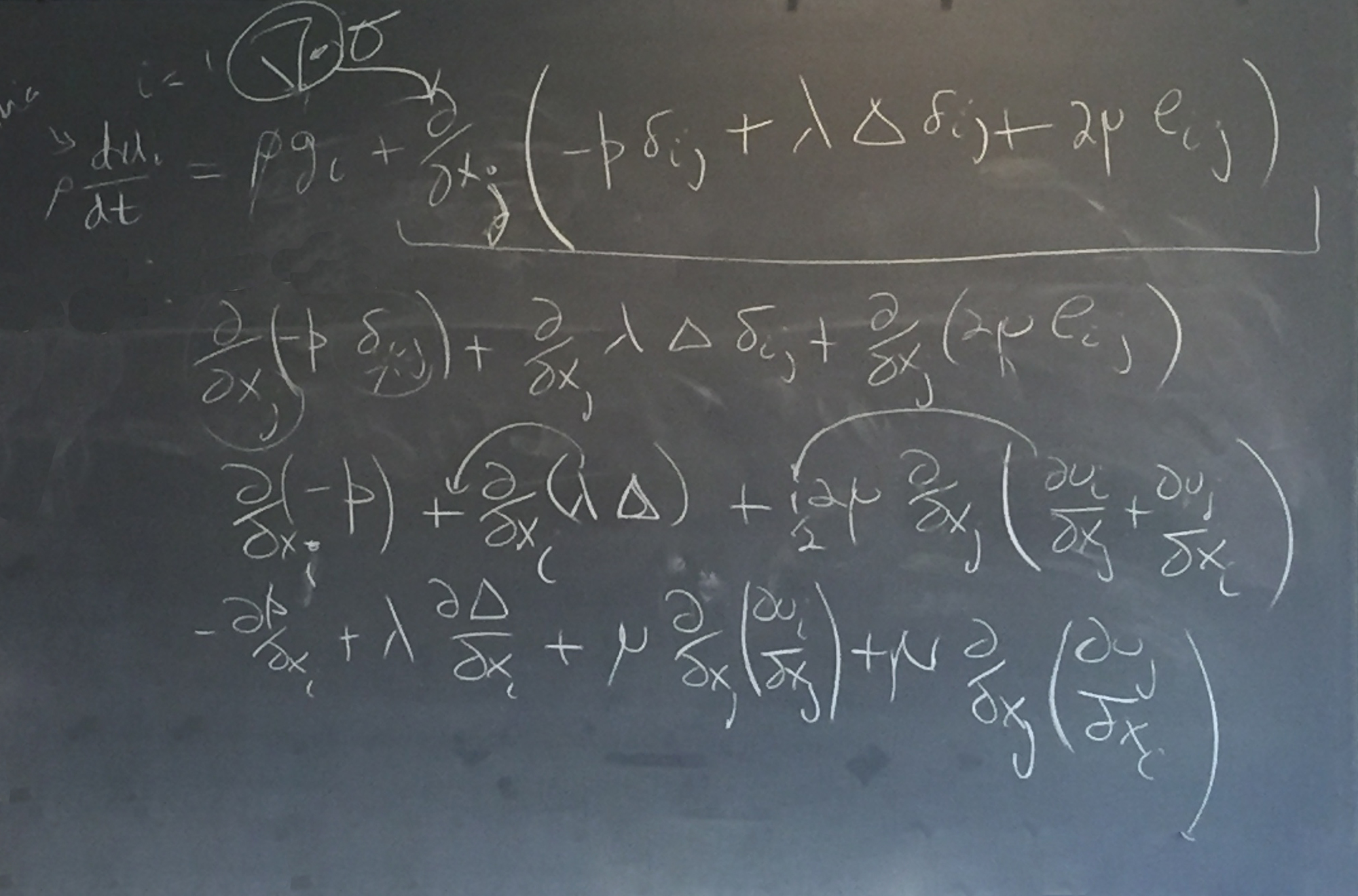
Chris then continued performing additional algebraic transformations to convert to:
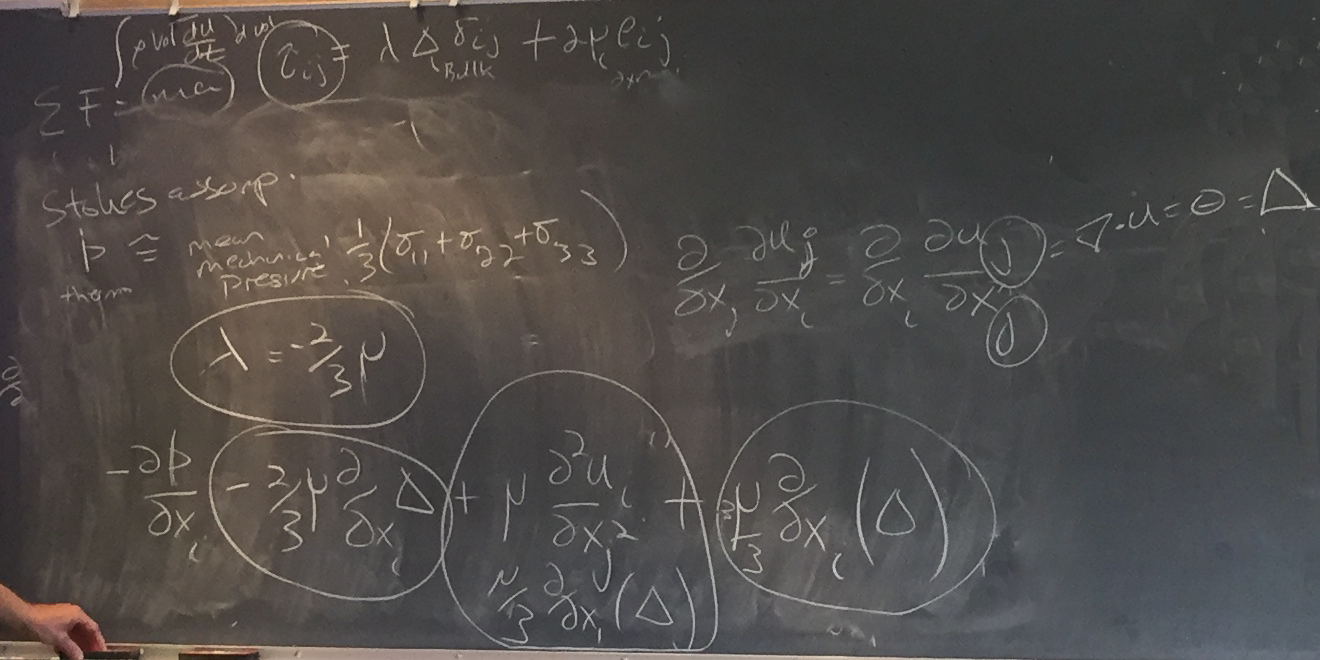
And then additional simplifications to get to a final momentum equation (which would be repeated three times for X values of 1, 2, and 3):

Chris reminded the students that advection has two effects. He had students visualize sitting on a deck looking off to the distance on a hot summer day when an airmass comes to cool off the air dramatically. The top term below is the advection felt as a change in temperature, while the bottom term is the advection felt as a wind (called power):
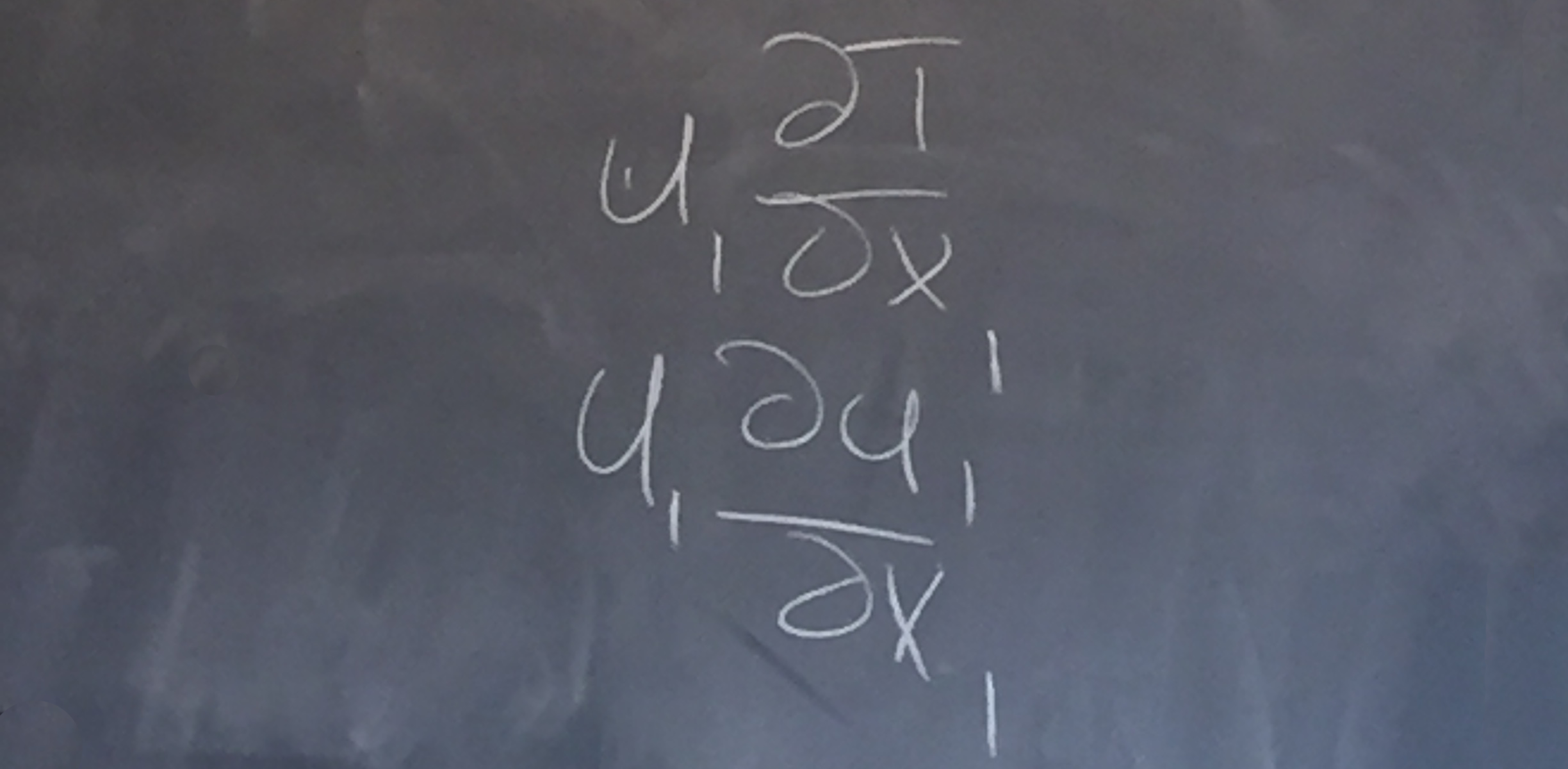
Chris wrote out the momentum equation for the case of i=2 (full momentum would include the i=1 and i=3 cases as well):
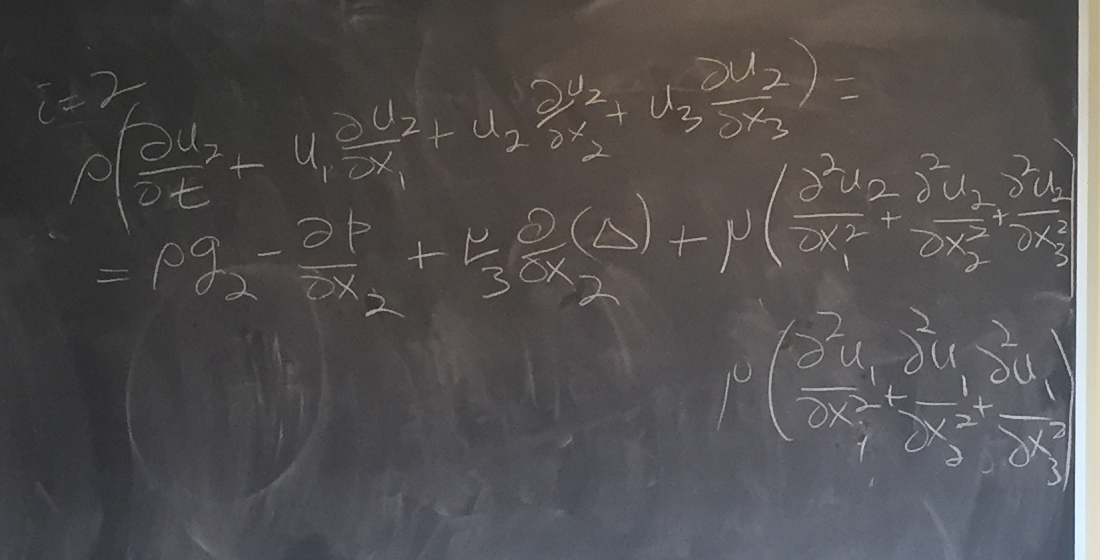
Chris finished up the class by pointing out the distinction of ρ and p as being comprised of a mean (scalar) and perturbation function and substituting them into the momentum equation.
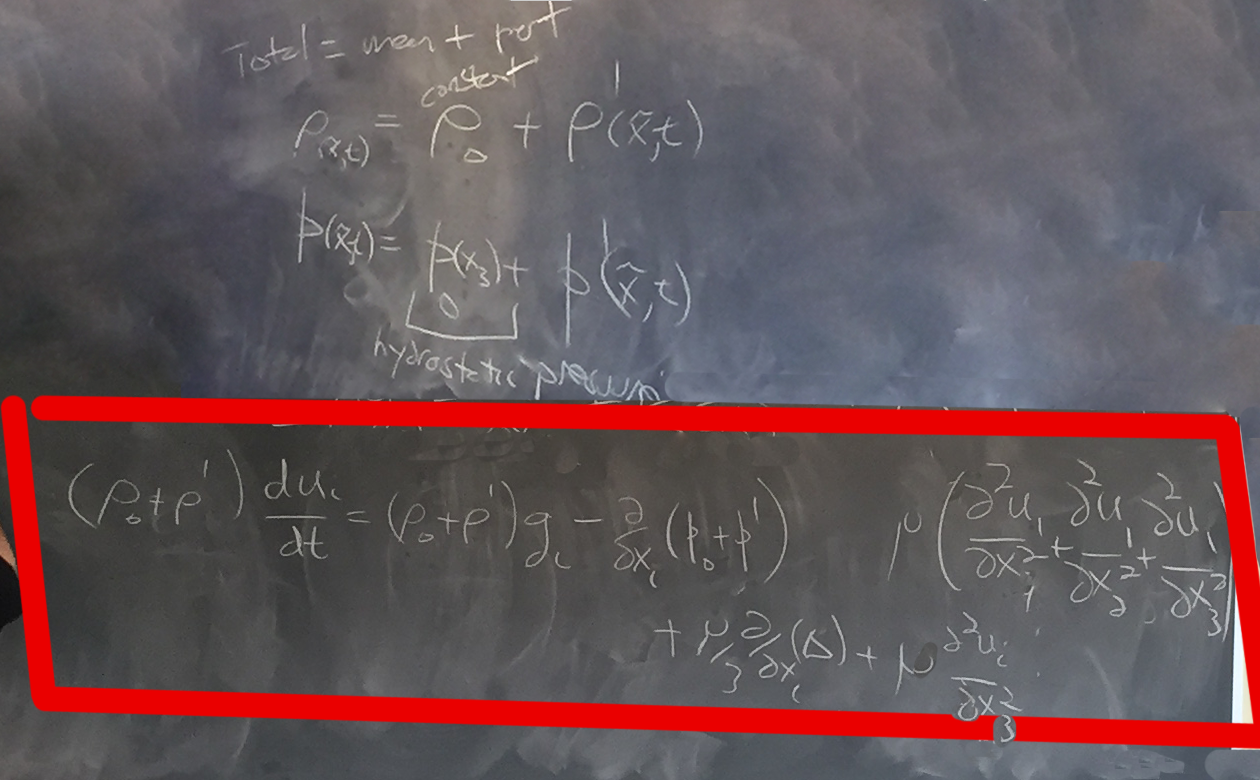
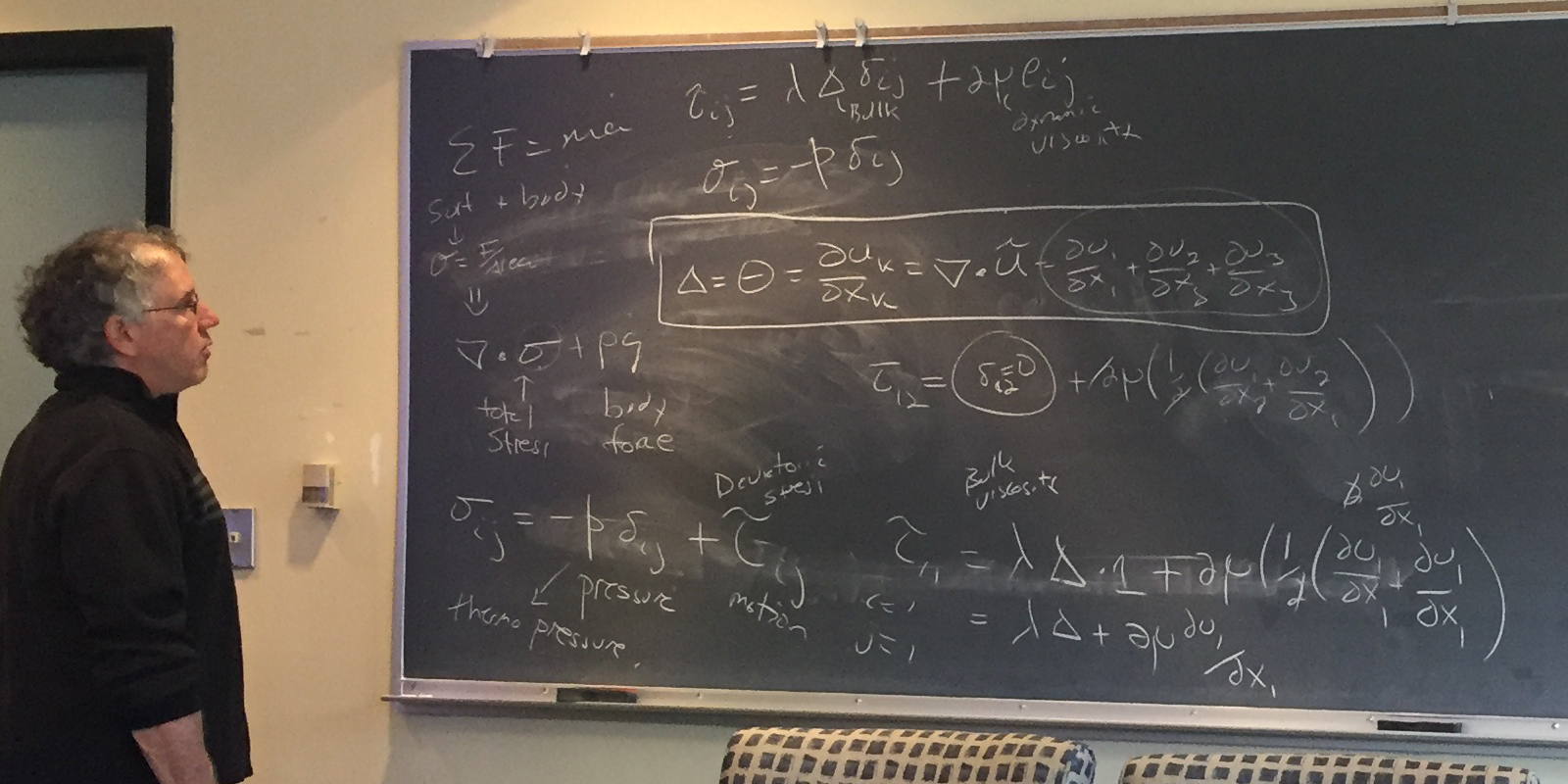
Chris then worked on the expansion of dui/dt:
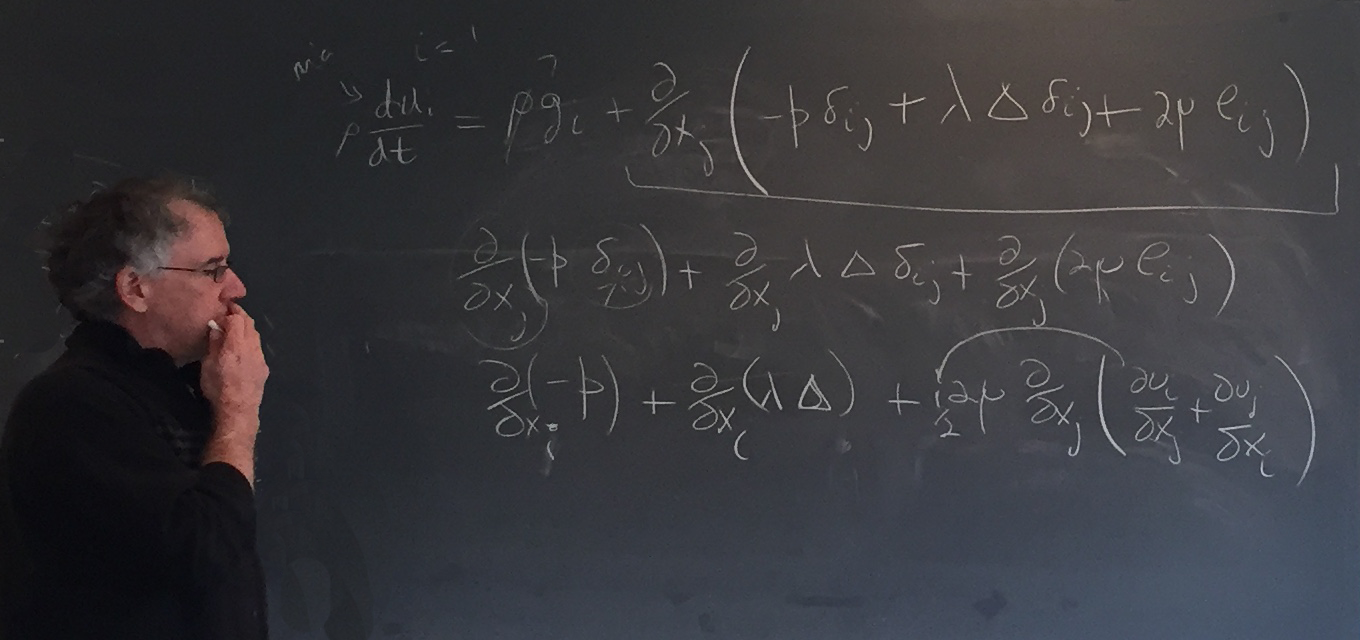
with the simplification of converting subscript j to i for a specific choice of axis (line 2 to 3 above).
Then, Chris pulled out some terms to prepare for simplifying the full momentum equation (line 3 to 4 below):
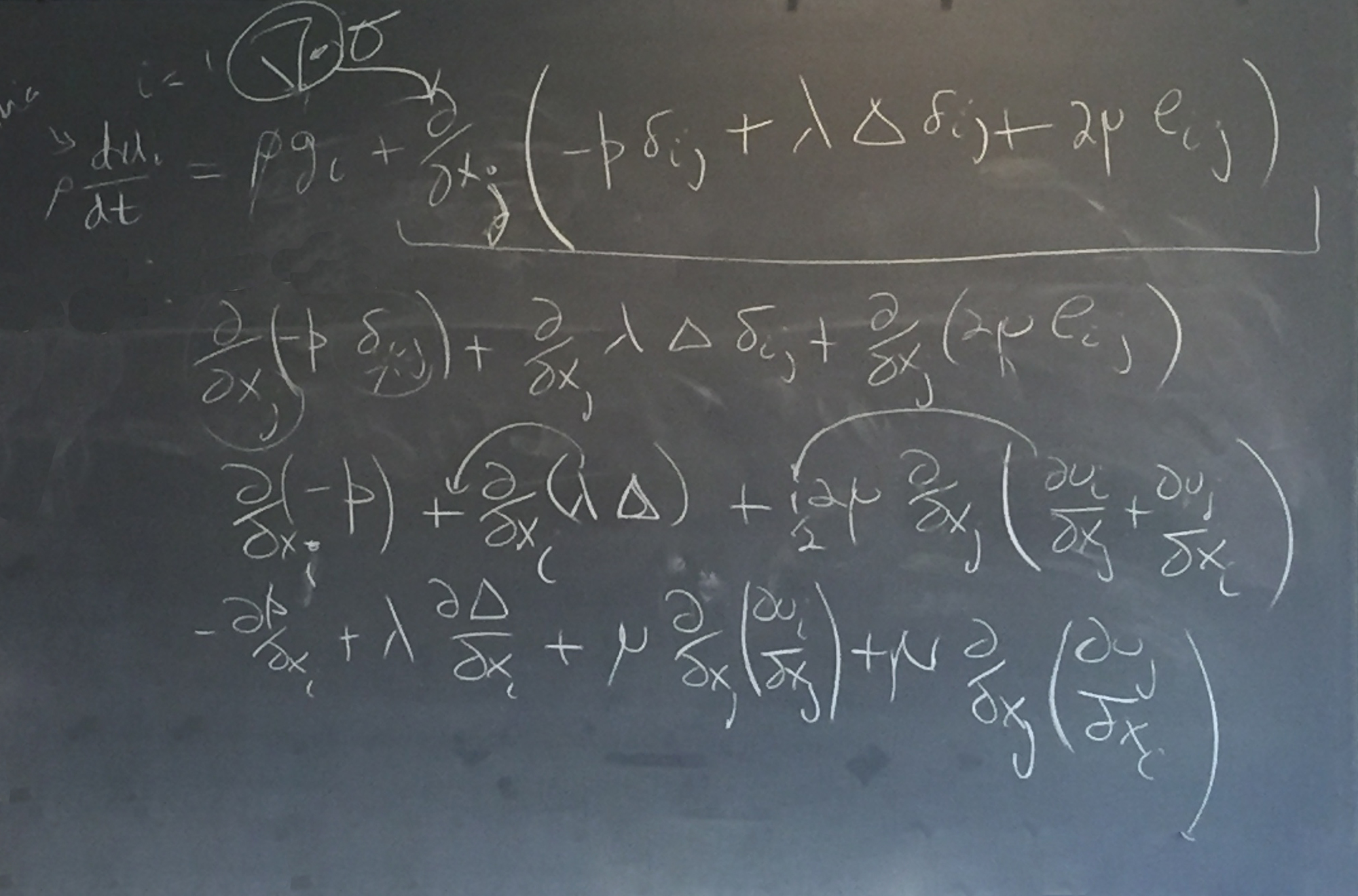
Chris then continued performing additional algebraic transformations to convert to:
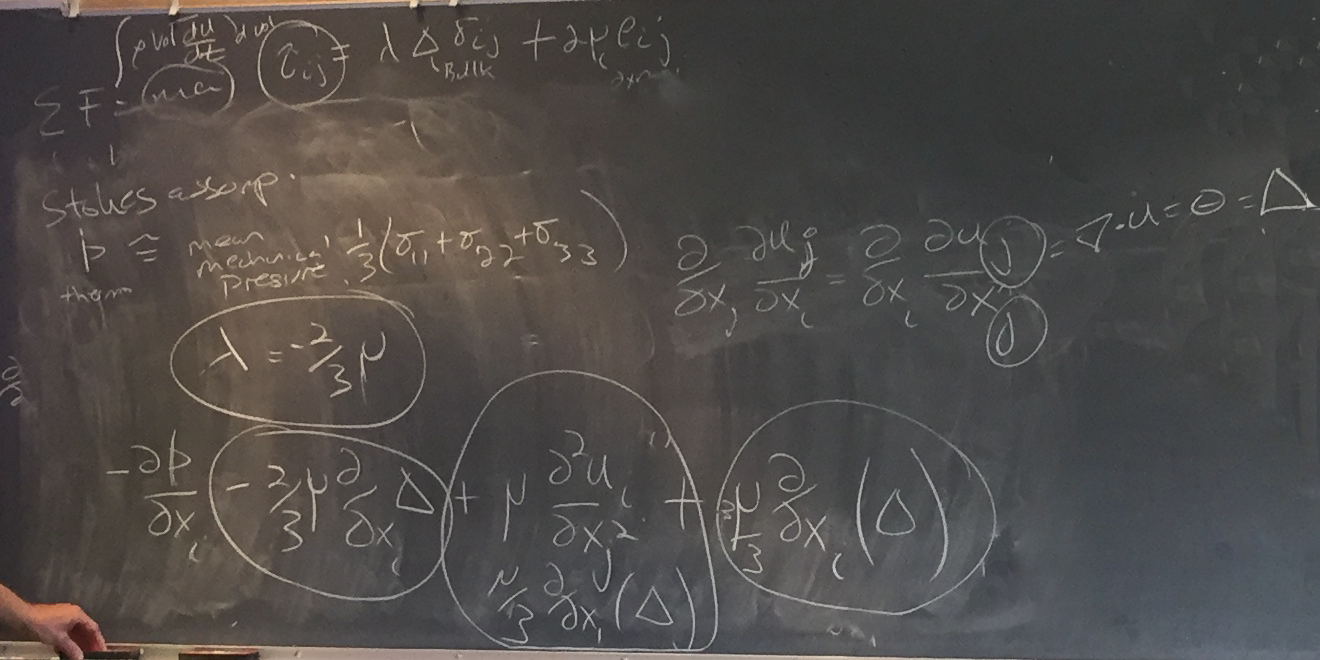
And then additional simplifications to get to a final momentum equation (which would be repeated three times for X values of 1, 2, and 3):

Chris reminded the students that advection has two effects. He had students visualize sitting on a deck looking off to the distance on a hot summer day when an airmass comes to cool off the air dramatically. The top term below is the advection felt as a change in temperature, while the bottom term is the advection felt as a wind (called power):
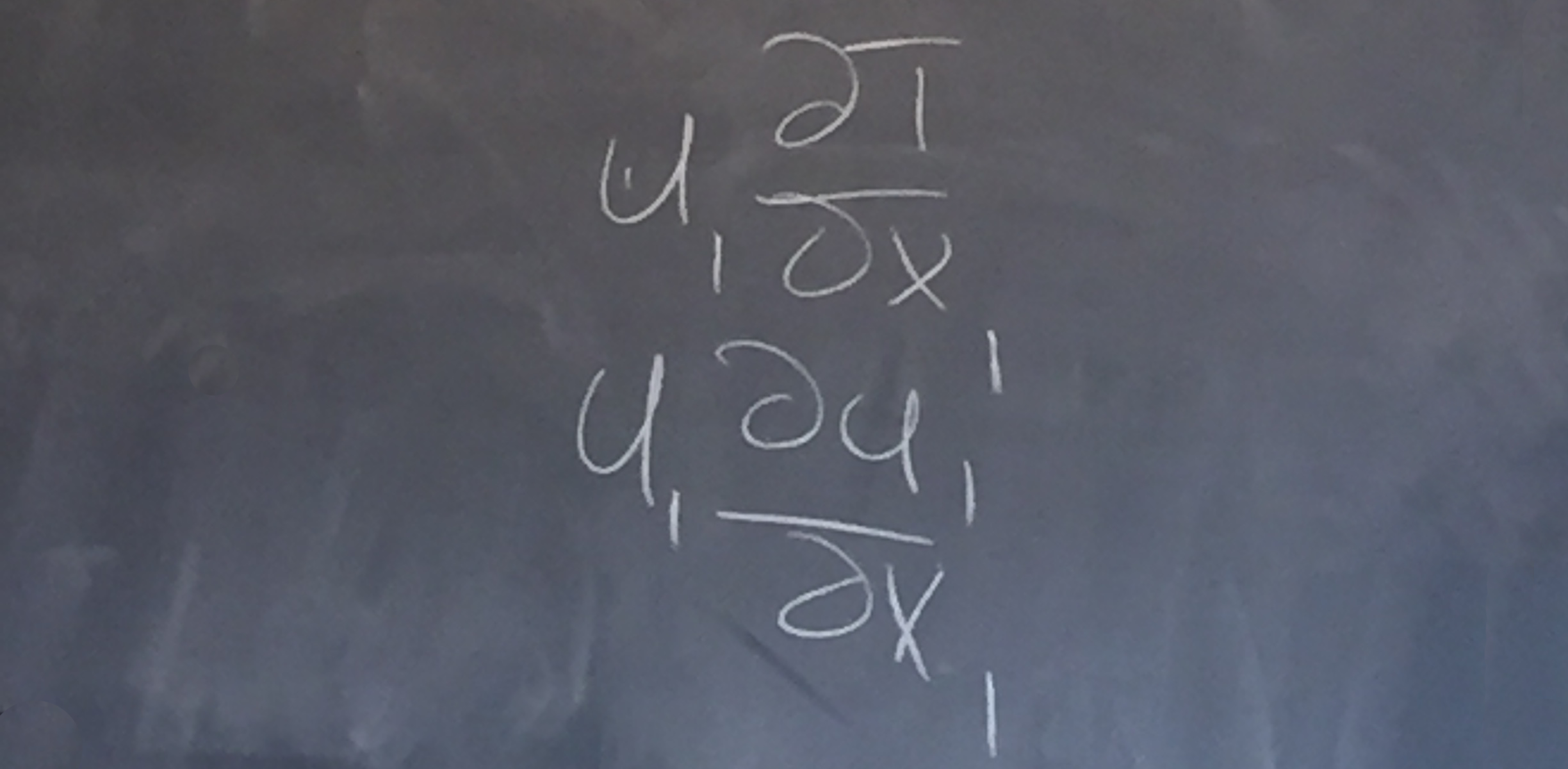
Chris wrote out the momentum equation for the case of i=2 (full momentum would include the i=1 and i=3 cases as well):
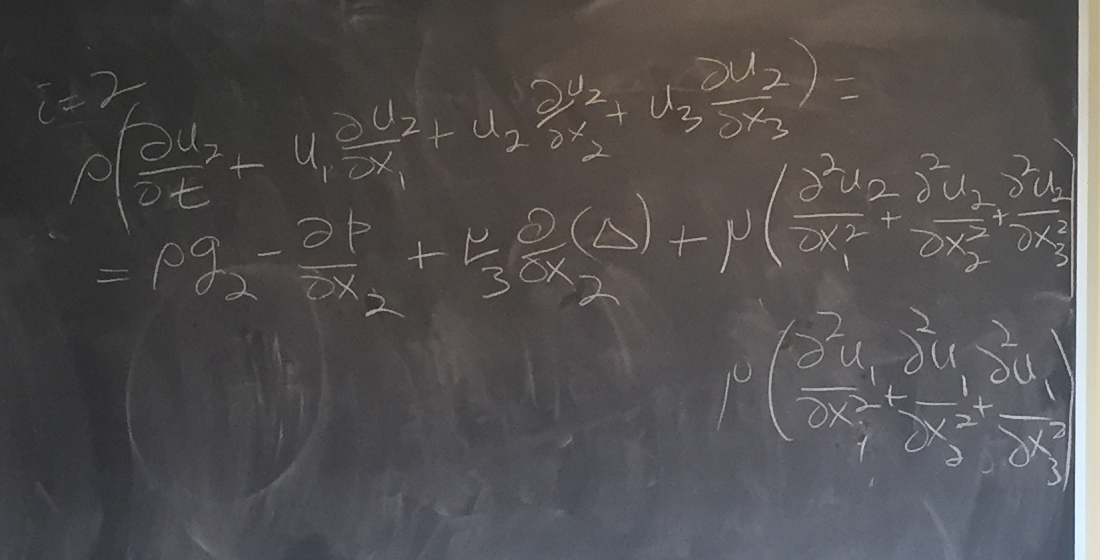
Chris finished up the class by pointing out the distinction of ρ and p as being comprised of a mean (scalar) and perturbation function and substituting them into the momentum equation.