Class on April 8, 2019
Students started class investigating visual representations of sheer on a parcel of water. Sheer happens when μ(δu1/δxn) for one face is
different than μ(δu1/δxn) for it's opposite face (where n can be 1, 2, or 3). It's not a matter of the magnitude of
μ(δu1/δxn) so a situation like:
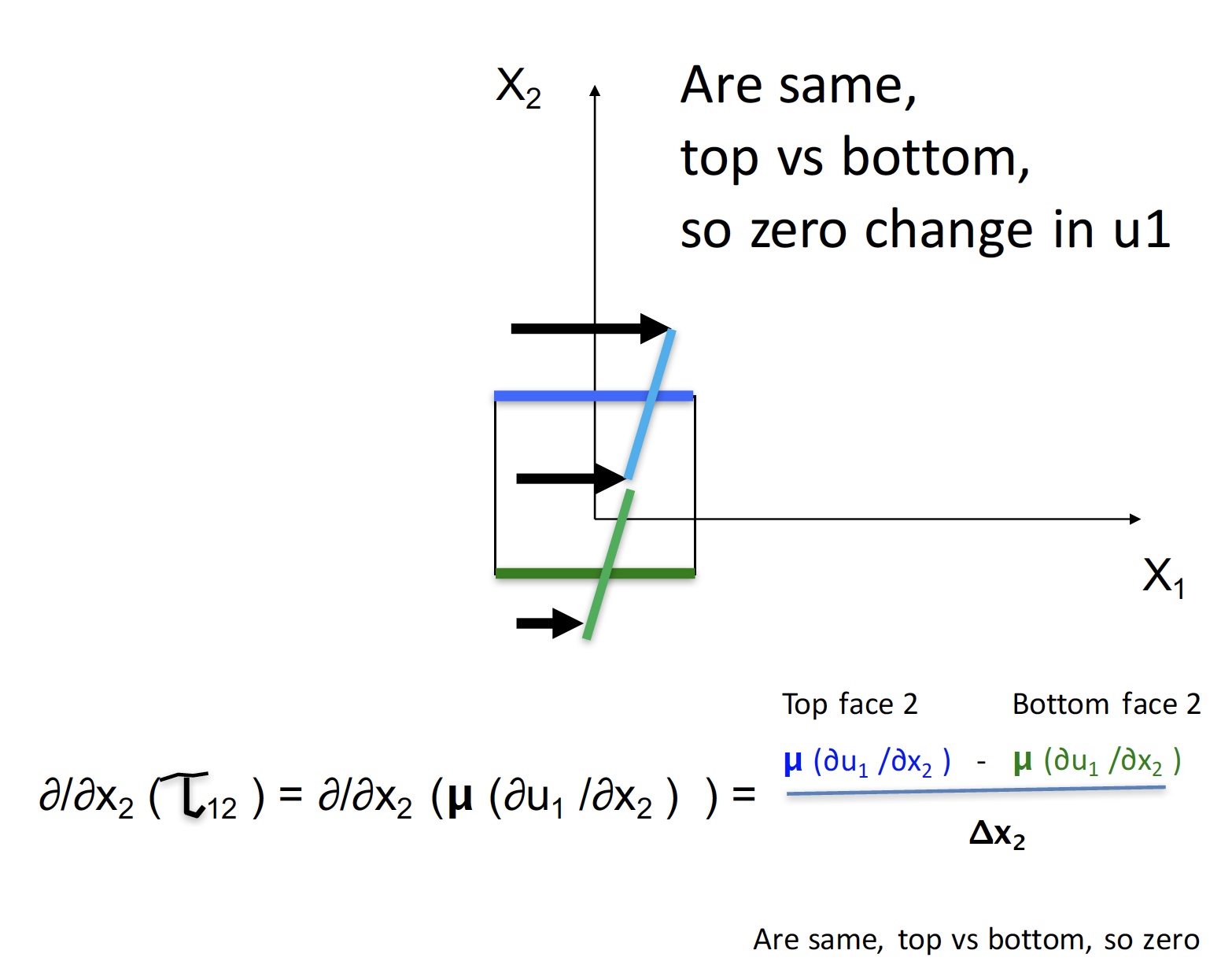
creates no sheer, while a situation like:
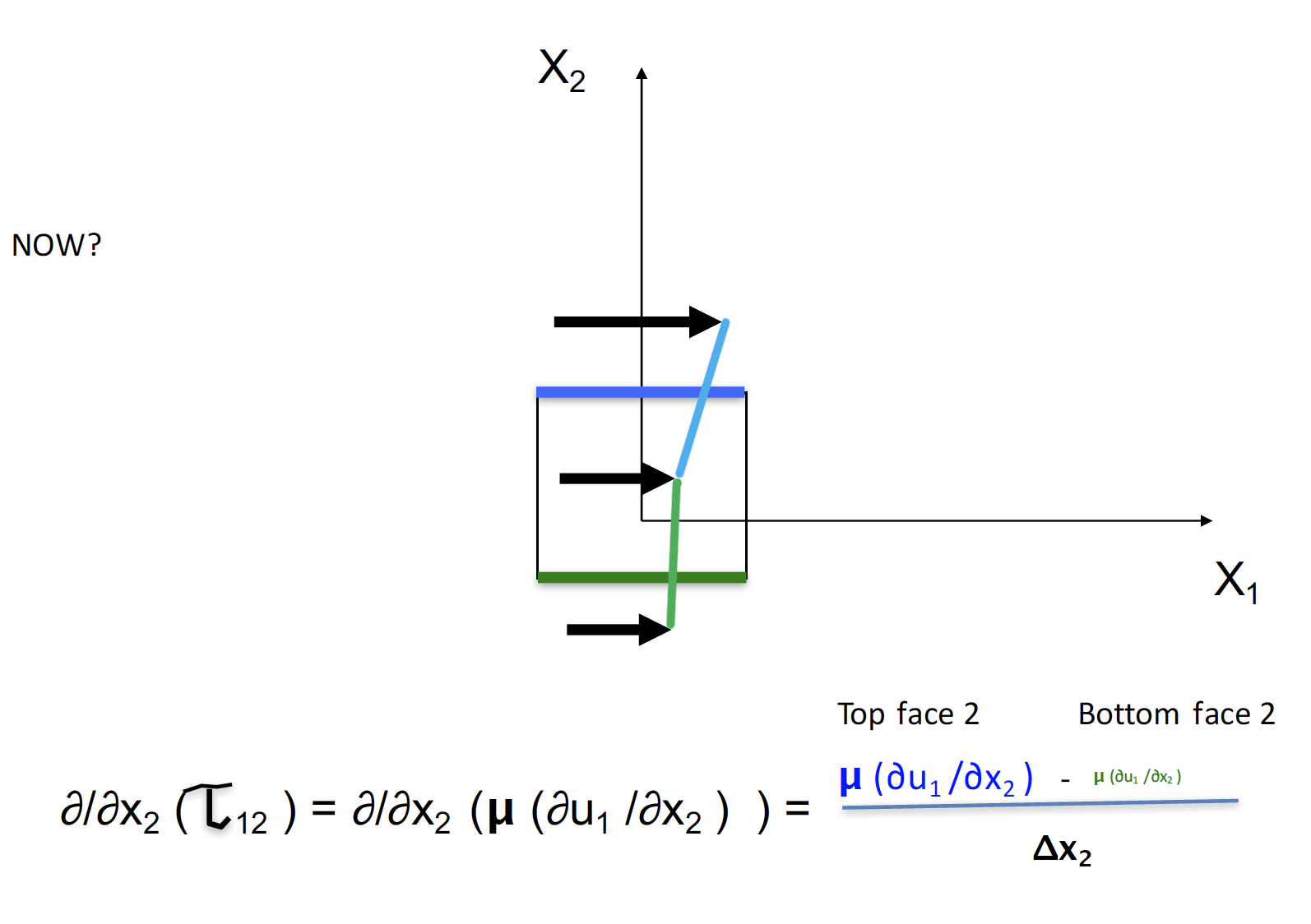
creates sheer on the parcel in the x1 direction.
Students then considered advection in conjunction with diffusion. When the the temperature diffusion coming towards a parcel is identical to the temperature diffusion heading away from the parcel, there is no effect on the parcel by diffusion. We can diagram the combined effect (using the advection sheer from the previous image above) in the diagram here:
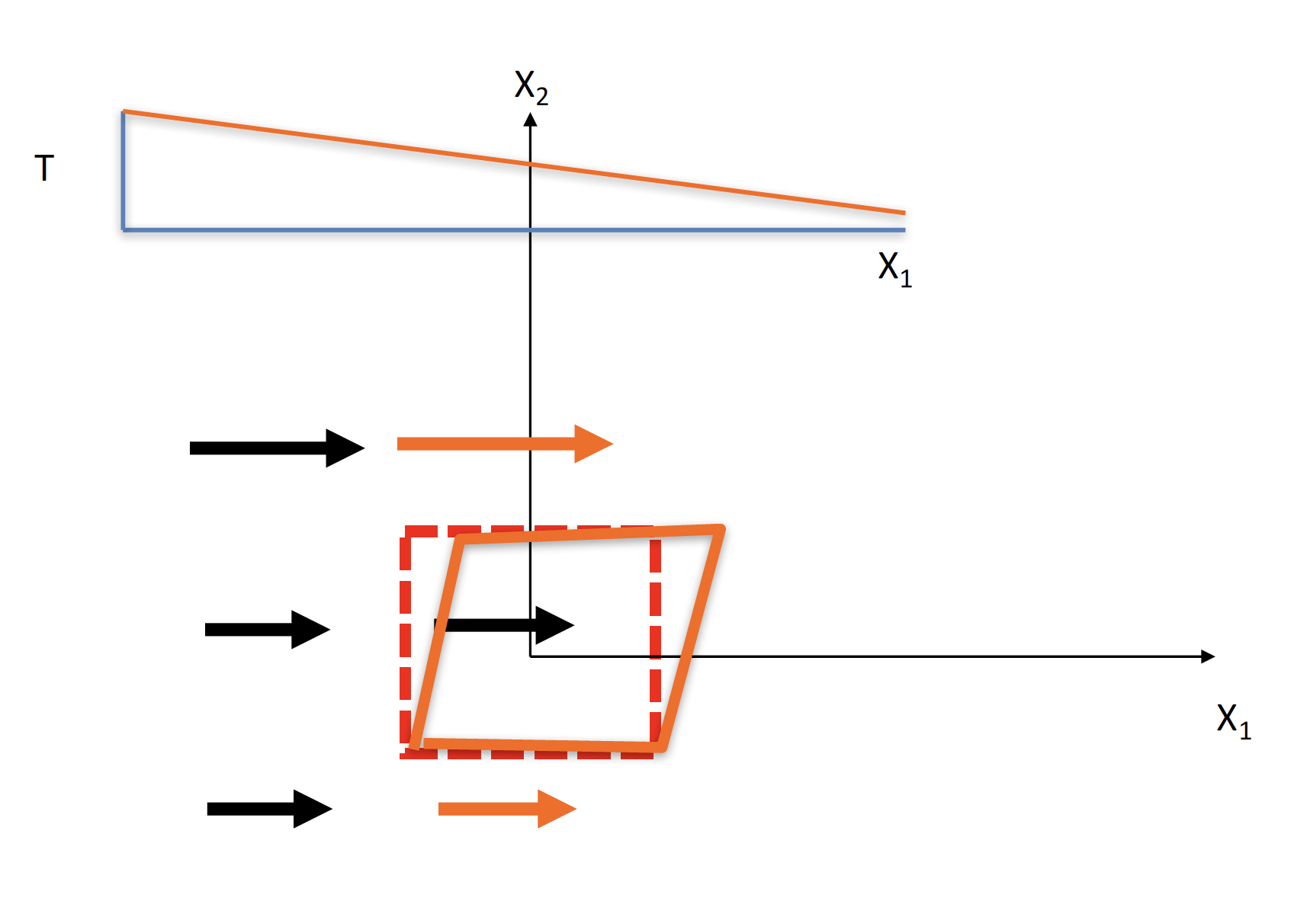
which shows diffusion having no effect in the top of the diagram, the sheer creating the parallelogram in the bottom of the diagram above.
We can combine the X2 faces sheer with a normal stress in the X1 faces (seen in green below) while keeping diffusion neutral:
There is symmetry of normal and sheer forces in any of the X1, X2, or X3 faces combinations. For example, X1 faces sheer with a normal stress in the X2 faces:
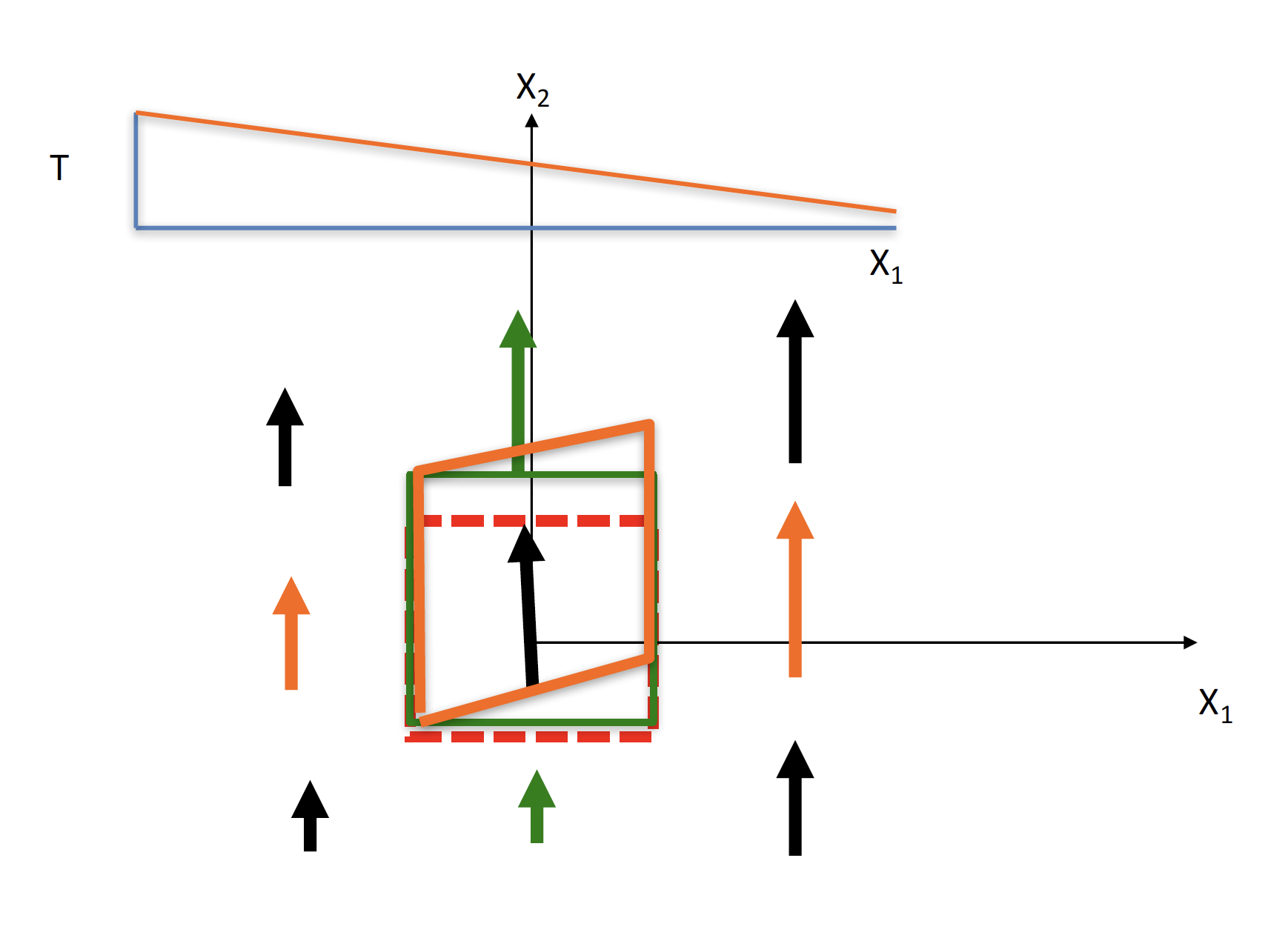
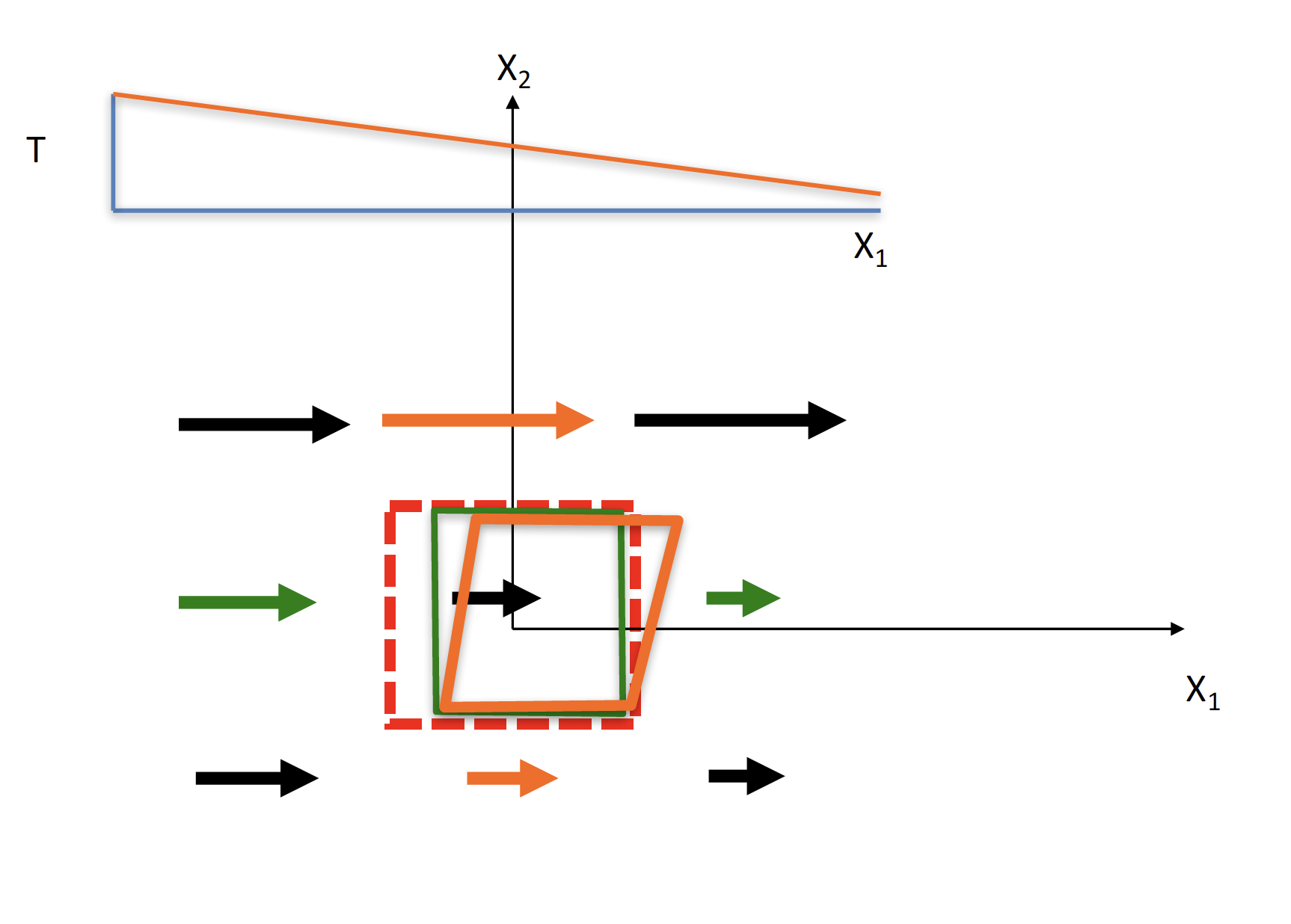
We can then start to diagram increasingly complicated diagrams of the energy equation at work. For example, in this diagram:
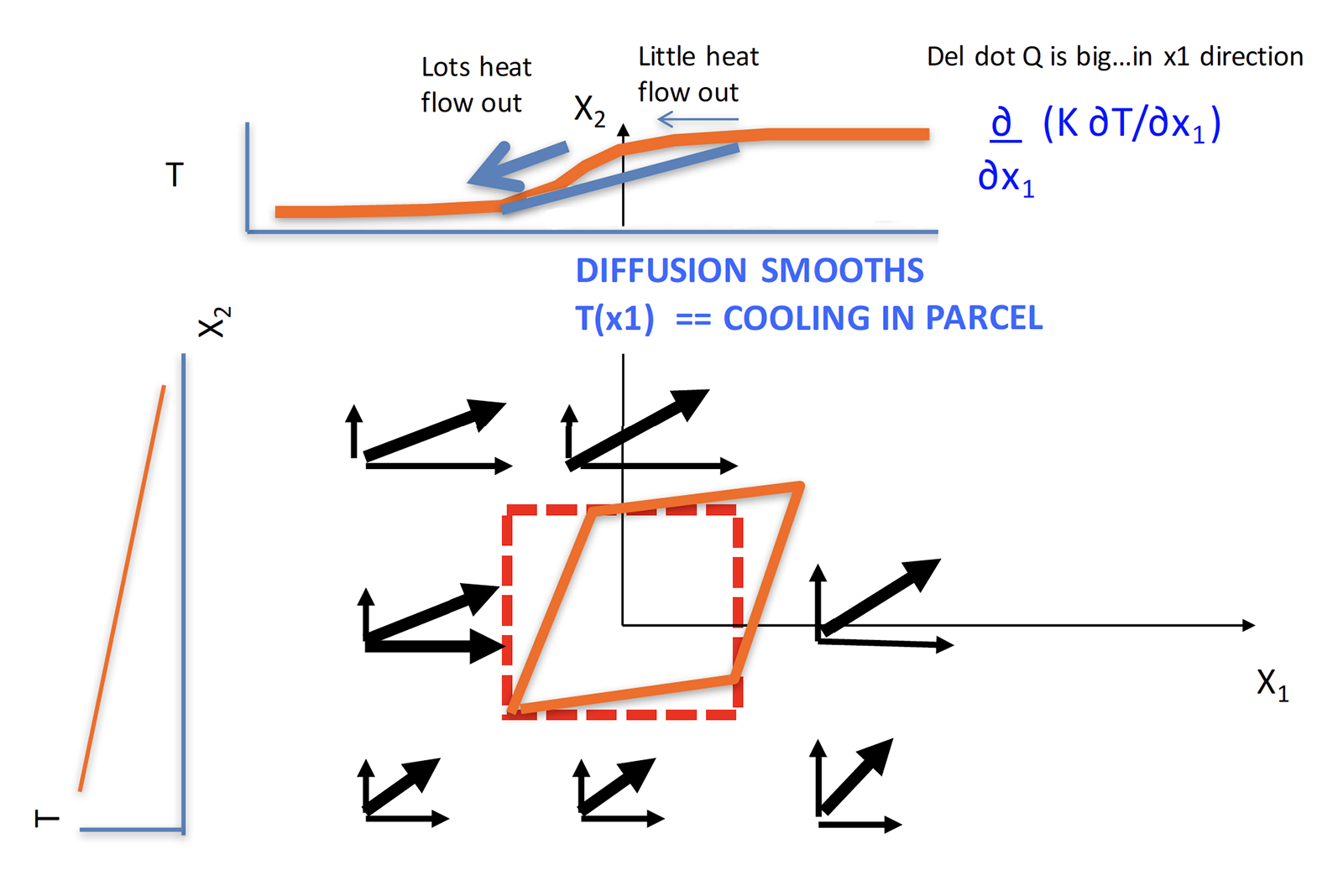
diffusion in the X2 direction is neutral, but in the X1 direction heat is diffusing to the left. The advection is counteracting the diffusion by creating combination of sheer and normal force on the parcel in the resultant shape of the orange quadrilateral.
Students spent the rest of the class trying to visualize diffusion and advection effects on a parcel of water for all three X1, X2, or X3 axes and the six surface faces orthogonal to them. The goal of the class is to be able to see such diagrams in the mind's eye, while also being fluent in the math that describes them, and being able to embed the formulas in code to enable simulation and modeling analyses. With enough repetition working all three tasks, insight into hydrothermal dynamics gets solidified and can be used when investigating bodies of water for understanding of significant phenomena.

creates no sheer, while a situation like:

creates sheer on the parcel in the x1 direction.
Students then considered advection in conjunction with diffusion. When the the temperature diffusion coming towards a parcel is identical to the temperature diffusion heading away from the parcel, there is no effect on the parcel by diffusion. We can diagram the combined effect (using the advection sheer from the previous image above) in the diagram here:

which shows diffusion having no effect in the top of the diagram, the sheer creating the parallelogram in the bottom of the diagram above.
We can combine the X2 faces sheer with a normal stress in the X1 faces (seen in green below) while keeping diffusion neutral:

There is symmetry of normal and sheer forces in any of the X1, X2, or X3 faces combinations. For example, X1 faces sheer with a normal stress in the X2 faces:

We can then start to diagram increasingly complicated diagrams of the energy equation at work. For example, in this diagram:

diffusion in the X2 direction is neutral, but in the X1 direction heat is diffusing to the left. The advection is counteracting the diffusion by creating combination of sheer and normal force on the parcel in the resultant shape of the orange quadrilateral.
Students spent the rest of the class trying to visualize diffusion and advection effects on a parcel of water for all three X1, X2, or X3 axes and the six surface faces orthogonal to them. The goal of the class is to be able to see such diagrams in the mind's eye, while also being fluent in the math that describes them, and being able to embed the formulas in code to enable simulation and modeling analyses. With enough repetition working all three tasks, insight into hydrothermal dynamics gets solidified and can be used when investigating bodies of water for understanding of significant phenomena.

