Class on March 8 2019
Chris put the students into teams of two and asked them to locate a parcel of water in the classroom based on a dimensionless L of 2 in both the east-west and north-south directions. The teams then did a series
of computations for their parcel in the context of the whole body of simulated water.
The situations built in complexity until a situation suggested a temporary paradox where L1 became 10 meters in one dimension and T became the other dimension of interest. Students had to find the value of parcels of water as time marched forward from 0 to 1:
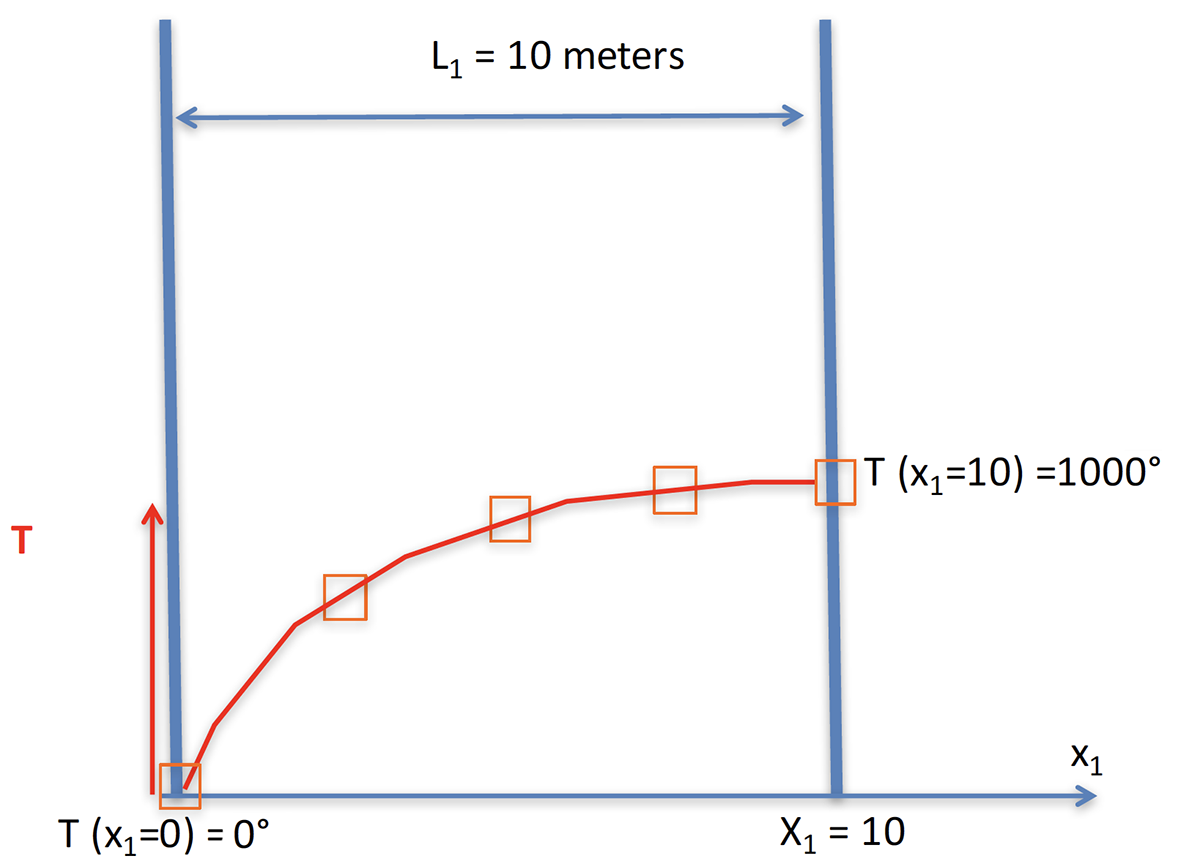
The paradox could be resolved with the introdution of advection.
Chris then presented an advection problem in an alternative, more typical, way of describing it:
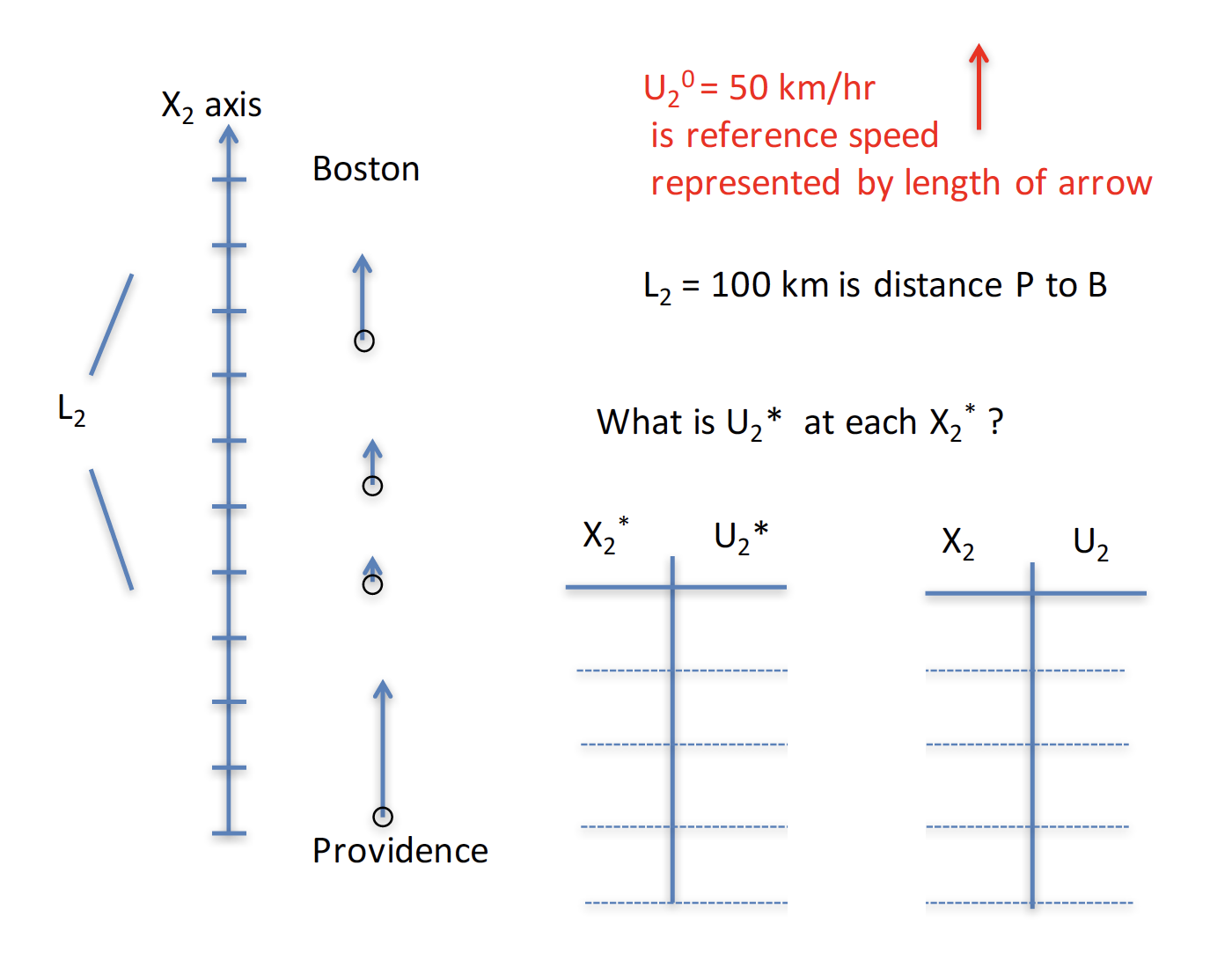
Students then calculated an estimated advection term at different locations between Providence and Boston along the X2 axis:
X2 (km) U2 (km/h)
Students were then asked to work on homework set #5:
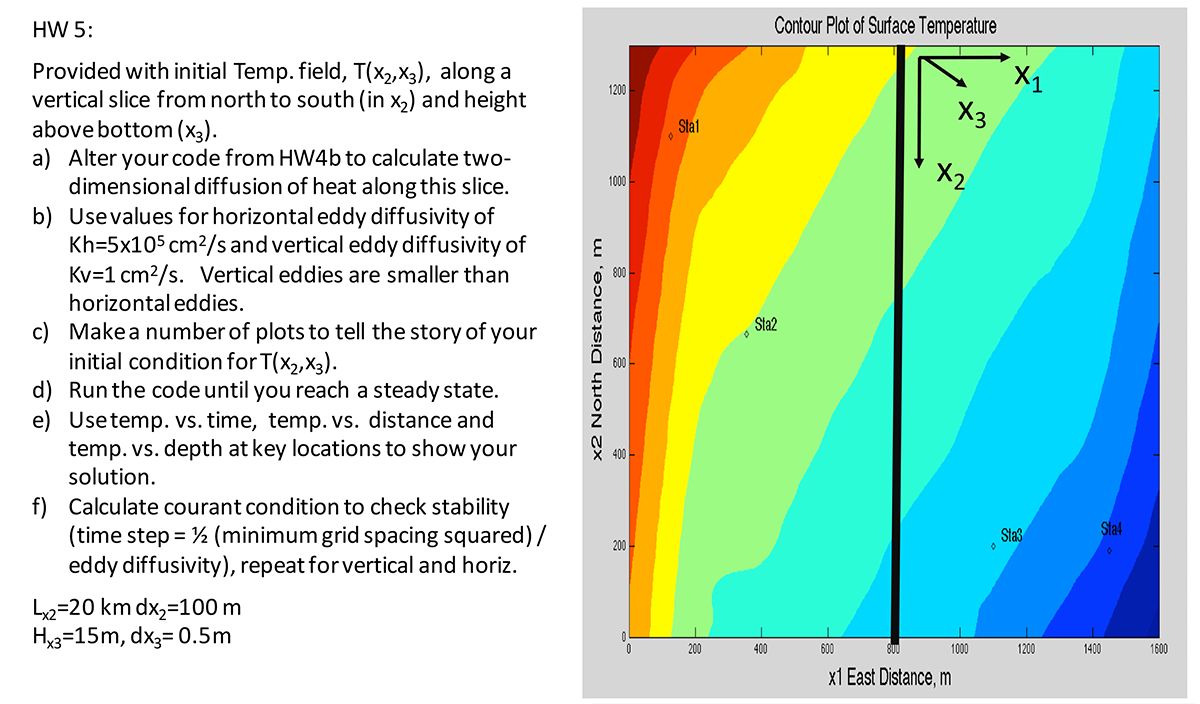
for the weekend and Spring Break. Homework set #6 would add advection mechanics to the 2-D molecular diffusion base coded in homework set #5.
The situations built in complexity until a situation suggested a temporary paradox where L1 became 10 meters in one dimension and T became the other dimension of interest. Students had to find the value of parcels of water as time marched forward from 0 to 1:

The paradox could be resolved with the introdution of advection.
Chris then presented an advection problem in an alternative, more typical, way of describing it:

Students then calculated an estimated advection term at different locations between Providence and Boston along the X2 axis:
X2 (km) U2 (km/h)
0 | 80 10 | 80 20 | 80 30 | 40 40 | 10 50 | 20 60 | 30 70 | 40 80 | 50 90 | 50 100 | 50The surface flow could be used to estimate time for moving from Providence to Boston:
The first 30km would be covered in 22.5 minutes (60 min/h * 30/80) The next 10km would be covered in 15 minutes (60 min/h * 10/40) The next 10km would be covered in 60 minutes (60 min/h * 10/10) The next 10km would be covered in 30 minutes (60 min/h * 10/20) The next 10km would be covered in 20 minutes (60 min/h * 10/30) The next 10km would be covered in 15 minutes (60 min/h * 10/40) The last 20km would be covered in 24 minutes (60 min/h * 20/50)so that the total estimated time in transit would be 186.5 minutes (3 hours and 6.5 minutes).
Students were then asked to work on homework set #5:

for the weekend and Spring Break. Homework set #6 would add advection mechanics to the 2-D molecular diffusion base coded in homework set #5.

