Class on September 18 2018
Jeremy provided an exercise and follow-on mathematical lecture on ecological efficiency concepts within a food web.
Students started the exercise by reading an assignment hand-out that described a marine food web which students as a group documented on the white board (seen here):
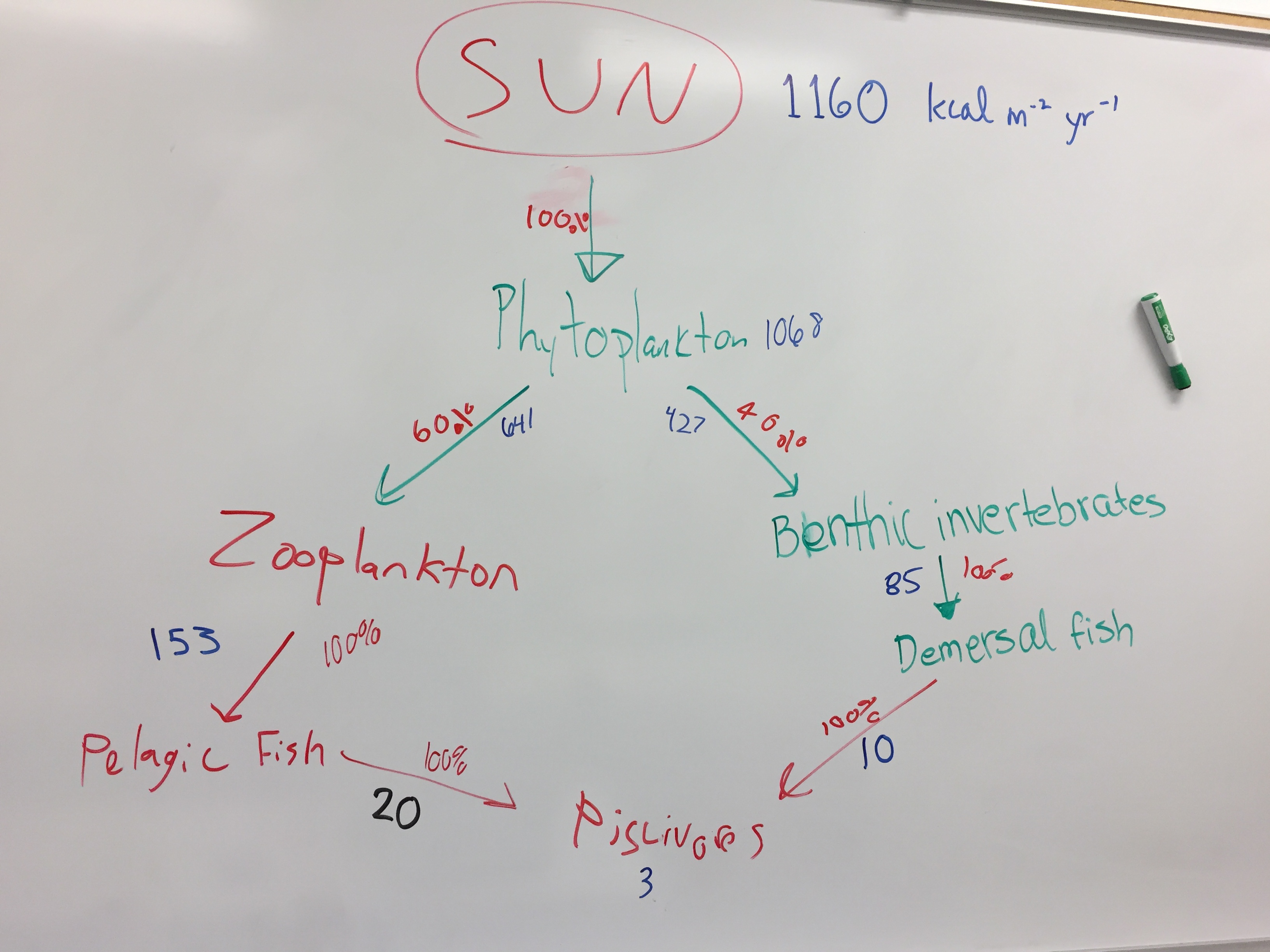
The hand-out provided efficiency ratios for each organism type in the web:
Phytoplankton: 92%
Zooplankton: 24%
Benthic invertebrates: 20%
Demersal fish: 11%
Pelagic fish: 13%
Piscivores: 10%
Jeremy handed out 1160 M&M candy units to the Phytoplankton team and asked that they feed their predators in the food web, using their 92% efficiency ratio to suggest quantity. As there was a known 60%-40% split between feeding Zooplankton and Benthic invertebrates, the Phytoplankton team passed on 641 (1160 * 0.6 * 0.92) M&M candy units (as symbolic of energy) to the Zooplankton team and 427 (1160 * 0.4 * 0.92) M&M candy units to Benthic Invertebrate team. Those teams then passed on their symbolic contributions to the Pelagic fish and Demsersal fish teams, which then forwarded on their contributions to the Piscivores.
As seen in the blue values recorded on the white board above, the Piscivores received 3 total M&Ms (out of 1160 provided by the sun - representing 1160 kcal m-2/year). Not very efficient as a human food choice!
Students were asked to imagine the process of doing such a labor intensive job for a significantly more complicated food web. Then Jeremy suggested there were mathematical methods to solve for energy distributions in a food web and provided an interactive session to develop those in an analog process for the exercise food web (a digital process would be provided in the following class).
The process unfolded on the white board as seen in the image below:
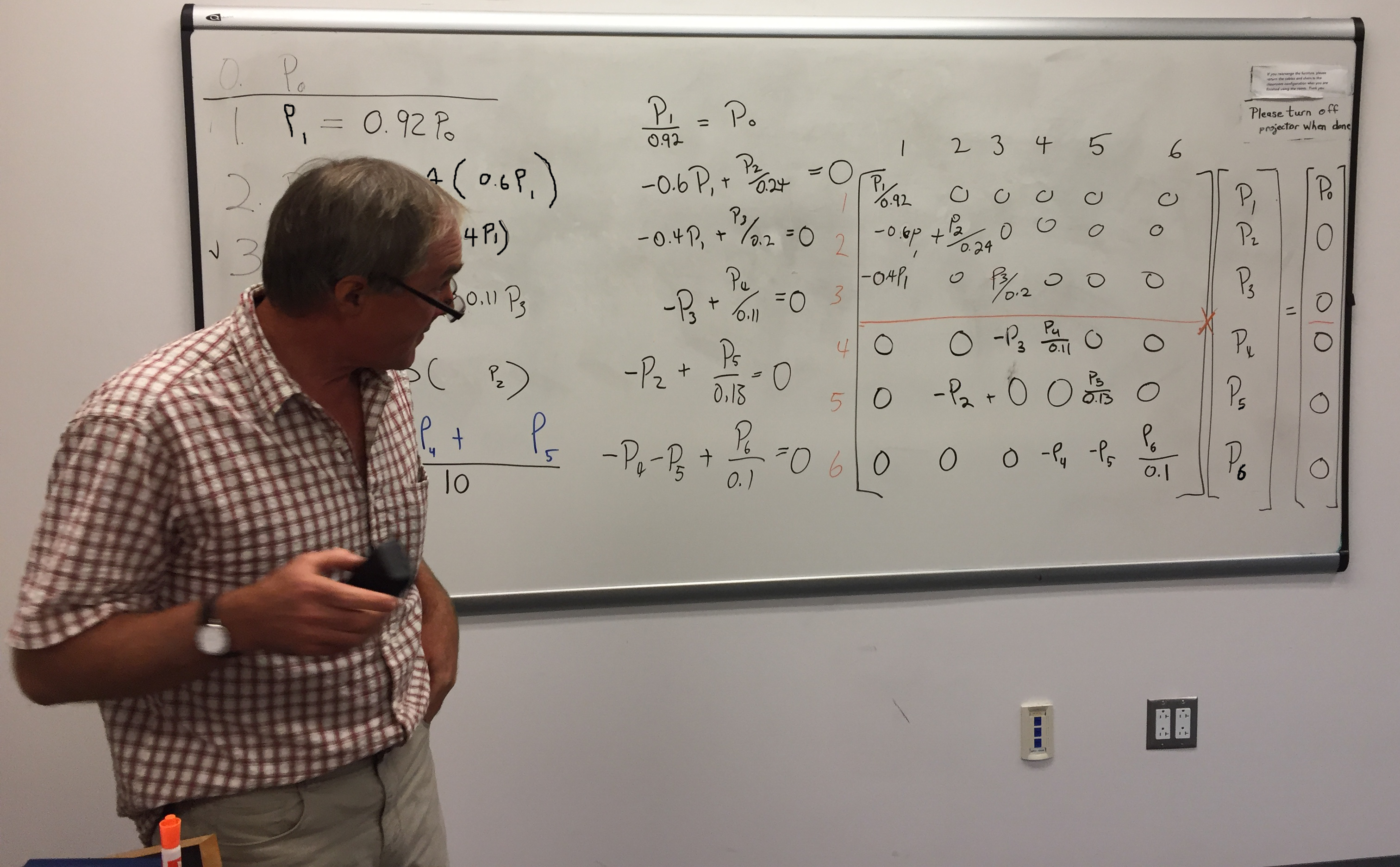
The known formula M.P = C formed the basis for a generation of three matrices to be solved through a linear algebra approach.
Solving is facilitated by multiplying both sides of the equation by M's identity matrix:
M*M-1.P = C*M-1
Since M*M-1.P reduces to P, we were able to calculate P by performing the matrix multiplication of C*M-1 with M-1 defined as:
Students were asked to prepare for Thursday's class by reading the Jupyter notes and installing Anaconda on the laptops they could bring to participate. Students were also told they could investigate the Python notes which would be the basis of Thursday's discussion.
A Web-based animation of the distribution of energy in the food web is provided for contemplation as well. In it, black dots represent the energy efficiency lost in the transfer from prey to predator.
Students started the exercise by reading an assignment hand-out that described a marine food web which students as a group documented on the white board (seen here):

The hand-out provided efficiency ratios for each organism type in the web:
Phytoplankton: 92%
Zooplankton: 24%
Benthic invertebrates: 20%
Demersal fish: 11%
Pelagic fish: 13%
Piscivores: 10%
Jeremy handed out 1160 M&M candy units to the Phytoplankton team and asked that they feed their predators in the food web, using their 92% efficiency ratio to suggest quantity. As there was a known 60%-40% split between feeding Zooplankton and Benthic invertebrates, the Phytoplankton team passed on 641 (1160 * 0.6 * 0.92) M&M candy units (as symbolic of energy) to the Zooplankton team and 427 (1160 * 0.4 * 0.92) M&M candy units to Benthic Invertebrate team. Those teams then passed on their symbolic contributions to the Pelagic fish and Demsersal fish teams, which then forwarded on their contributions to the Piscivores.
As seen in the blue values recorded on the white board above, the Piscivores received 3 total M&Ms (out of 1160 provided by the sun - representing 1160 kcal m-2/year). Not very efficient as a human food choice!
Students were asked to imagine the process of doing such a labor intensive job for a significantly more complicated food web. Then Jeremy suggested there were mathematical methods to solve for energy distributions in a food web and provided an interactive session to develop those in an analog process for the exercise food web (a digital process would be provided in the following class).
The process unfolded on the white board as seen in the image below:
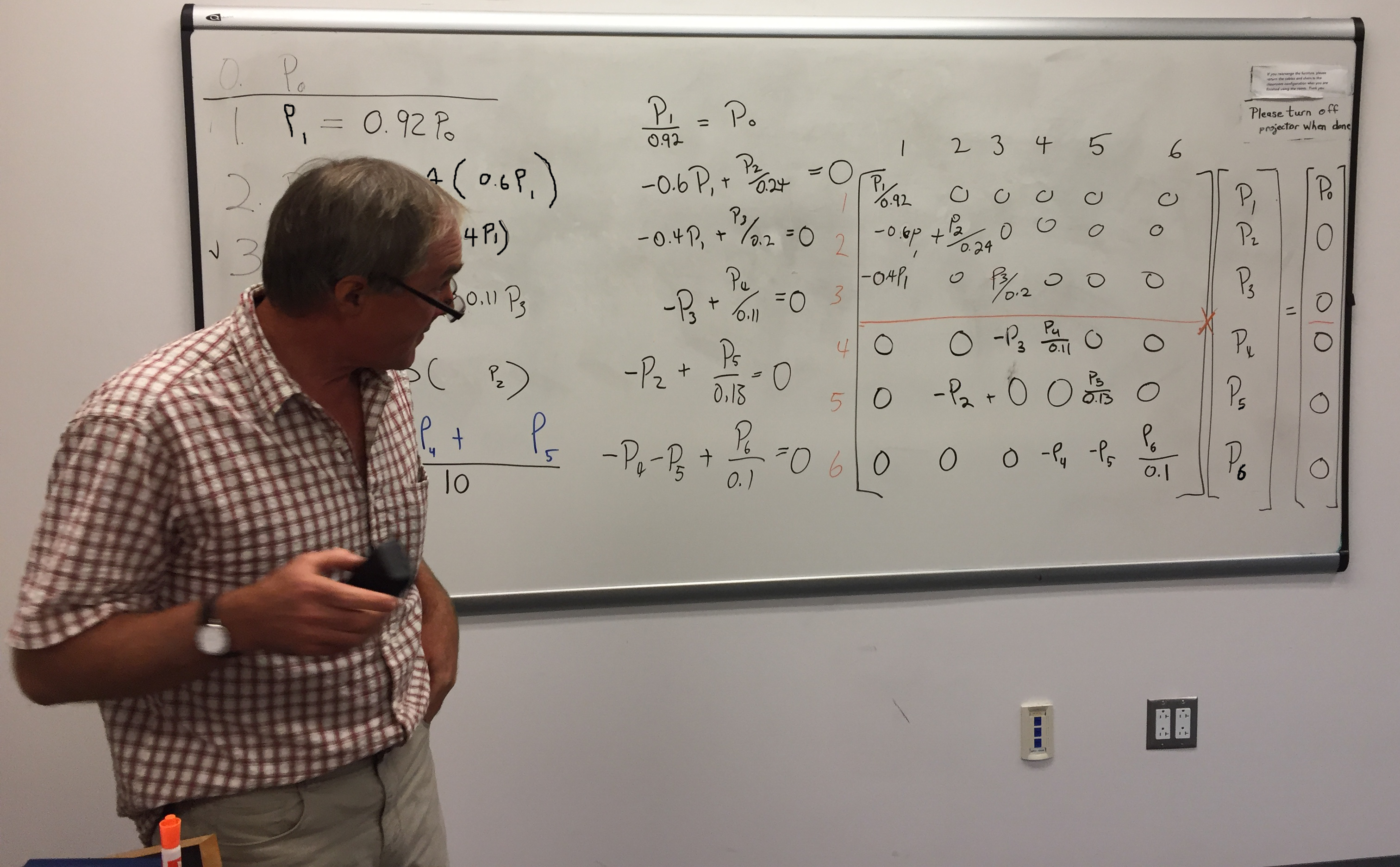
The known formula M.P = C formed the basis for a generation of three matrices to be solved through a linear algebra approach.
Solving is facilitated by multiplying both sides of the equation by M's identity matrix:
M*M-1.P = C*M-1
Since M*M-1.P reduces to P, we were able to calculate P by performing the matrix multiplication of C*M-1 with M-1 defined as:
[[ 1.08695652 0 0 0 0 0 ] [ -0.6 4.16666667 0 0 0 0 ] [ -0.4 0 5 0 0 0 ] [ 0 0 -1 9.09090909 0 0 ] [ 0 -1 0 0 7.69230769 0 ] [ 0 0 0 -1 -1 10 ]]and C defined as:
[ 1160 0 0 0 0 0 ]we can see the multiplcation leads to:
[ 1067.2 153.6768 85.376 9.39136 19.977984 2.9369344 ]which aligns well with rounded/truncated solutions performed by transferring whole M&M candy units.
Students were asked to prepare for Thursday's class by reading the Jupyter notes and installing Anaconda on the laptops they could bring to participate. Students were also told they could investigate the Python notes which would be the basis of Thursday's discussion.
A Web-based animation of the distribution of energy in the food web is provided for contemplation as well. In it, black dots represent the energy efficiency lost in the transfer from prey to predator.

