Class on September 6 2018
Students were welcomed to class and introduced to the syllabus by the faculty.
Rob led an ice-breaker exercise that looked at the interactive population dynamics of predator and prey. The exercise simulated the population dynamics in the lives of stripers and sharks. Students contemplated how both predator and prey interact with each other and affect the number of individuals in a given region. If there are no predators and the food source is unlimited (an unlimited carrying capacity) then the population of stripers can grow in a non-linear fashion.
Three groups of students filled out an Excel spreadsheet with population counts upon performing 13 rounds of a simulation. Each round consisted of:
Sharks (2.5 inch x 2.5 inch squares of paper) that were randomly dropped onto a sea patch (11 inch x 17 inch sheet of paper) covered in stripers (1 inch x 1 inch squares of paper) to represent sharks catching and eating stripers, which is necessary for the sharks to survive and reproduce. In each round, a varying number of sharks were dropped onto a varying population of striper. The populations of sharks and stripers in each round then depend on the previous round's results according to these rules for the paper-based simulation.
For example:
A striper does not survive if it is eaten by sharks, which is represented by a shark touching or partially covering that striper after being thrown onto the sea patch. A striper reproduces (generates a single additional striper in the next round) only if, after the entire population of sharks is thrown onto the meadow, it has not been eaten. However, once the striper population reaches a total of 75, no more stripers can reproduce. If no stripers are left surviving after a round, three new stripers repopulate the sea patch by migration for the next round.
A shark does not survive if, after being thrown onto a sea patch, it has eaten (is touching or partially covering) two or less stripers. A shark reproduces if it eats 3 or more stripers after a single throw into the meadow. It generates an additional shark in the next round for every multiple of 3 stripers that it is partially covering. (Example: 3 stripers = 1 shark, 5 stripers = 1 shark, 6 stripers = 2 shark). If no sharks survive a round, a single new shark migrates to the sea patch, and attempts to catch stripers in the next round.
The results for the paper-based simulation include a chart that looks like:
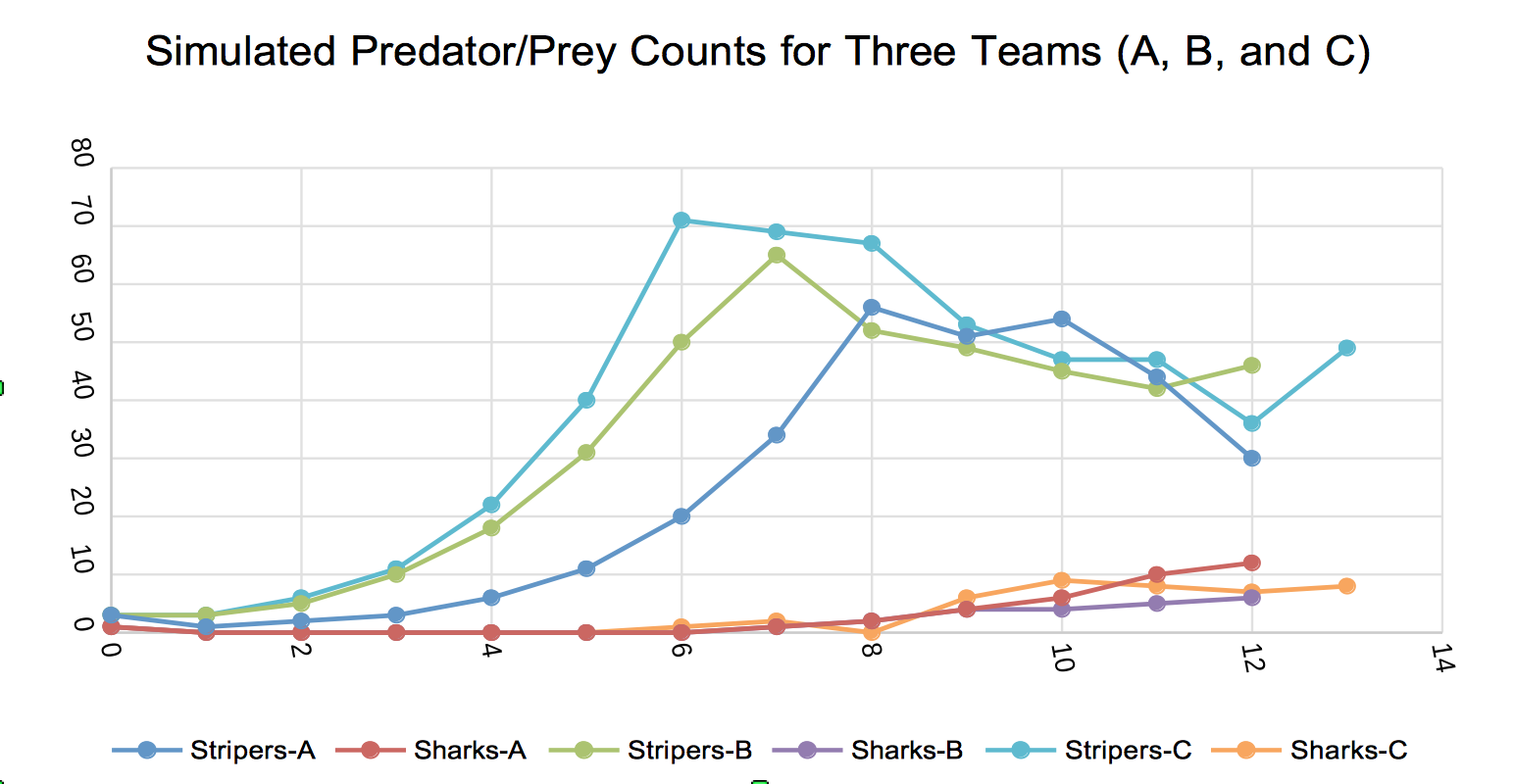
where the population dynamics for sharks and stripers look similar over time.
Rob led an ice-breaker exercise that looked at the interactive population dynamics of predator and prey. The exercise simulated the population dynamics in the lives of stripers and sharks. Students contemplated how both predator and prey interact with each other and affect the number of individuals in a given region. If there are no predators and the food source is unlimited (an unlimited carrying capacity) then the population of stripers can grow in a non-linear fashion.
Three groups of students filled out an Excel spreadsheet with population counts upon performing 13 rounds of a simulation. Each round consisted of:
Sharks (2.5 inch x 2.5 inch squares of paper) that were randomly dropped onto a sea patch (11 inch x 17 inch sheet of paper) covered in stripers (1 inch x 1 inch squares of paper) to represent sharks catching and eating stripers, which is necessary for the sharks to survive and reproduce. In each round, a varying number of sharks were dropped onto a varying population of striper. The populations of sharks and stripers in each round then depend on the previous round's results according to these rules for the paper-based simulation.
For example:
A striper does not survive if it is eaten by sharks, which is represented by a shark touching or partially covering that striper after being thrown onto the sea patch. A striper reproduces (generates a single additional striper in the next round) only if, after the entire population of sharks is thrown onto the meadow, it has not been eaten. However, once the striper population reaches a total of 75, no more stripers can reproduce. If no stripers are left surviving after a round, three new stripers repopulate the sea patch by migration for the next round.
A shark does not survive if, after being thrown onto a sea patch, it has eaten (is touching or partially covering) two or less stripers. A shark reproduces if it eats 3 or more stripers after a single throw into the meadow. It generates an additional shark in the next round for every multiple of 3 stripers that it is partially covering. (Example: 3 stripers = 1 shark, 5 stripers = 1 shark, 6 stripers = 2 shark). If no sharks survive a round, a single new shark migrates to the sea patch, and attempts to catch stripers in the next round.
The results for the paper-based simulation include a chart that looks like:

where the population dynamics for sharks and stripers look similar over time.

